摘要:本文根据轨道交通网络存在大量换乘路径的特点,改进深度优先搜索算法得出站点间换乘路径的有效出行时间。基于 AFC 数据得到的乘客进出闸机时刻,利用仿真方法确定乘客与列车在时间和路径的接续关系,同时考虑始发乘客和换乘乘客路径选择行为的差异,将二者区分配流。动态更新先到乘客利用换乘路径的出行时间,并以更新后的时间作为后续出发乘客的路径选择依据。结果表明该仿真方法可以有效反映乘客的出行过程,具有较高的配流精度。
关键词:轨道交通;动态客流分配;时刻表;AFC 数据
引言
城市轨道交通运营严格遵循时刻表,基于时刻表进行网络配流、准确反应客流流动状况和各次列车在各路段的载运情况,对提高城市轨道交通精细化管理水平具有重要意义。
近年来国内外学者对城市轨道交通配流的研究主要集中网络均衡配流模型构建和仿真配流模型构建方面。网络均衡配流模型构建方面文献[1]引入开销系数和惩罚系数来描述拥挤度和换乘对乘客心理感知的影响,降低了换乘路径的选择概率。文献[2]分析了乘客出行的 AFC(自动票务收集系统:Automatic Fare Collection System)数据,提出了基于 AFC 数据的乘客出行路径选择行为估计方法。文献[3]通过建立列车时刻表连接网络将多路径网络下的乘客路径选择问题转化 为了生成多路径并确定路径权重的指派问题,并考虑了高峰时段乘客无法上车对乘客路径选择行为的影响。文献[4]在上述基础上进一步考虑了列车座位利用率对客流分配结果的影响。文献[5] 建立了轨道交通时空配流模型并利用相继平均法求解。
相较于客流分配模型,基于仿真方法的分配模型在乘客出行行为刻画、分配过程模拟和动态瞬时客流分布统计方面具有较大的优势。在轨道交通网络结构、列车时刻表和客流的 OD 情况明确的条件下,能够反映出乘客对于列车的交互反馈情况,具有较高的适应性。
文献[7]和文献[8],按时间顺序推演乘客与列车的交互关系,逐步遍历某一时刻之前所有进入地铁乘客的出行状态,实时模拟乘客的出行行为。文献[9]通过输入 AFC 数据,列车时刻表和路网数据,模拟轨道交通网络下路网、乘客与列车三个主体间的交互过程,并考虑了大小交路和列车容量限制的影响,按时间递推顺序进行了网络动态配流。同时针对仿真方法受配流规模制约较大这一缺点,提出了基于列车离站的仿真推演方法,简化了乘客出行过程,提高了计算效率。文献[10]为了简化以乘客为主体进行仿真时繁琐的标定过程,基于系统中乘客的出行轨迹完全依赖于列车运行这一特点,提出了类似于乘客动态仿真算法的列车动态仿真配流算法,以列车到站时间为统计时间间隔进行仿真时间的推进,统计该时刻站台乘客情况按照先到先发进行配流,实现了乘客与列车的交互过程。
本文以上述研究成果为基础,考虑了 AFC 数据、列车时刻表与乘客到达时间的匹配关系。现有的仿真方法未能反映列车容量限制导致乘客无法上车时产生的额外等待时间,以及车站换乘人数变化造成的乘客换乘时间变化。针对这些缺陷,本文提出了考虑换乘路径出行时间随客流时空特征变化的动态配流仿真方法,具体内涵为:一旦有乘客利用某条换乘路径完成了出行,则根据该乘客的出行情况动态更新该换乘路径的出行时间,后续出发乘客的候选路径中包含该路径时,以最近一次更新后的出行时间作为后续出发乘客路径选择的依据,从而反映换乘路径出行时间随时间的变化。该方法可以克服既有配流方法的缺陷,进而更有效地实现乘客与列车的匹配,得到研究时段内各列车在各路段的载客人数以及列车搭载乘客在各站的换乘情况。本文以成都地铁为例对模型及算法进行了验证和分析。
1 问题描述
1.1 基于时刻表的城市轨道交通配流问题
基于时刻表进行网络配流时,需要明确网络中列车的开行情况和乘客到达情况。列车开行情况包括列车始发时刻和在各站的到、发时刻。乘客出行情况包括乘客进出站时间和乘客 OD,该数据可由轨道交通 AFC 数据获得。已知上述数据后确定各线路各次列车在各路段的客流量是本文的研究问题。
1.2 模型假设
(1)不考虑突发状况的产生,各线路列车运行稳定,按图行车;
(2)假设同一站点乘客从任意进站闸机口到站台的距离相同,不考虑不同进站闸机口与站台间的差异情况;
(3)乘客乘车时先到先上;
(4)乘客选择出行路径后中途不变更路径;
(5)结合文献[11],假设同一车站乘客由闸机口到站台与由站台到闸机口的走行时间服从同一分布。
2.2 轨道交通动态配流模型由
2.1 得到 OD 间的候选路径后,对乘客个体的路径选择行为进行配流,其中始发站上车乘客基于匹配出行时间的方法进行路径选择,而换乘站换乘乘客已于始发站选择完路径,其在换乘站的路径选择唯一,故将始发站上车乘客和换乘站换乘乘客配流情况分开研究。
2.2.1 始发乘客-列车配流模型
配流模型按配流过程依次分为 5 个部分:(1)基于 AFC 数据得到的出行时间确定始发乘客选择路径;(2)根据始发乘客选择路径确定乘客可搭载列车候选集;(3)根据列车载客量和站台人数确定各列车实际可搭载的始发乘客数量;(4)确定始发乘客的复合参数;(5)列车驶离后统计站点剩余人数。
4 案例分析
4.1 参数输入
截至 2018 年 5 月成都地铁网络结构如图 2。以 2018 年 5 月 1 日成都地铁的 AFC 数据作为乘客出行情况输入。并进行下述处理:
1) 剔除始发站与终到站相同的数据;
2)若 AFC 数据显示的乘客出行时间小于最短路出行时间,剔除该数据。结合 AFC 数据得出 6:00~12:00 间合计利用轨道交通完成 422262 次出行,以 1 分钟为步长进行配流。
4.2 求解结果
利用 MATLAB R2018a 编程路径遍历算法以及配流算法,所有运算均在 CPU 为 Inter Core i7-10710 3.3 GHz内存为16G的64位电脑上运行。
出行时间路径长度扩大系数取 1.8 ,一共得到候选路径 55258 条,其中换乘路径 50850 条。配流算法运行时间为 376.7 秒。
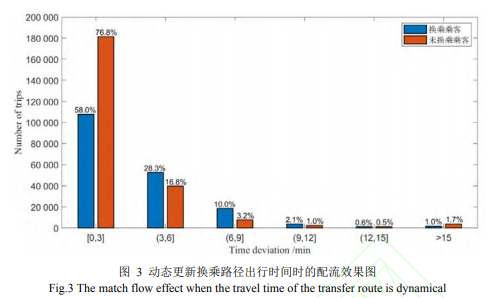
动态更新换乘路径出行时间时配流方法求得的乘客出行时间与由AFC数据得到的乘客出行时间的偏离情况如图 3 所示。其中未换乘乘客因其出行过程相对简单,配流结果精度较高,出行时间误差小于 3 分钟的乘客占出行总数 76.8%,小于 6 分钟的占 93.6%。换乘乘客出行过程复杂,出行时间较长,不确定因素相对较多,误差小于 3 分钟的乘客占比为 58%,小于 6 分钟乘客的占比为 86.3%。
为了进一步验证动态更新换乘路径出行时间的配流模型及算法的优势和正确性,对比动态更新换乘路径出行时间和换乘路径出行时间取固定值时的配流精度。换乘路径出行时间取固定值时的配流精度如图 4 所示,其中换乘乘客的配流精度明显下降,误差在 0~3 分钟的乘客占比下降至 53.9%,同时因非换乘路径不涉及路径出行时间的更新,非换乘乘客的配流精度不变。另外,由表 1 可知动态更新换乘路径出行时间的配流方法在均方误差(MSE)、平均绝对误差(MAE)、标准差 (STD)方面均优于换乘路径出行时间取固定值时的配流方法。
6:00~9:00 间各线路上各次列车的配流结果如图 5~10 所示,可以得出研究时段内列车在途经各路段上载客量的变化情况。6:00~8:00 间各列车载客量逐渐增长,8:00 附近达到峰值,此后逐渐减小。并且 7 号线因首班车到达前有较多乘车在站台积聚,首班车客流量较大。各列车的载客量多在换乘站附近达到峰值,同线路同方向的列车载客量在不同路段间的变化规律具有一致性,但变化幅度随客流增大而增大。此外,因为网络中存在大量换乘乘客,不同线路间列车载客量的变化幅度大小在时间上有一定的同步性。
6:00~9:00 间各次列车上搭载乘客在途径换乘站的换乘人数如图 11~14 所示,由图可知相同线路在不同方向上的换乘乘客数量存在较大的差距,4 号线不同方向上同站换乘乘客数量差值最大可到 200 人以上。除了换乘站 101 外,其余换乘站均存在单列车换乘乘客人数大于 100 人的情况,站点 3、10、13、42、45、48、79、93 部分单列车搭载的换乘乘客数量在 200 人以上。站点 79 作为 10 号线上唯一的换乘站有大量乘坐 10 号线的乘客在该站换乘。站点 79 作为 10 号线上行方向始发站和 3 号线下行方向的始发站时不存在搭载乘客的换乘,故值为 0。
研究中发现路径出行时间多服从正态分布,因篇幅关系仅展示部分路径的出行时间分布,如图 17~20 所示,算例结果符合以往研究对路径出行时间分布规律的认识。
5 结论
本研究中将换乘客流加入换乘站的客流,同换乘站的客流按照先到先发顺序进行依次配流,更符合实际乘客出行情况。同时按照时间顺序对选定时刻下的停站列车进行配流,后上车乘客在先上车乘客的配流基础上进行配流,实现了二者间的互动。依据利用换乘路径完成出行乘客的出行时间动态更新换乘路径出行时间,作为后续乘客的路径选择基础,更准确有效地反应了乘客路径选择情况。得到的轨道交通网络客流分配情况与列车搭载乘客换乘情况对提高城市轨道交通的科学运营管理水平具有重要价值。——论文作者:胡剑鹏1,2,罗霞 1,2
参考文献:
[1] 陈坚, 王曼, 李和平, 等. 城市轨道交通网络乘客换乘路径选择行为模型[J]. 交通运输系统工程与信息, 2017, 17(6): 235-241. (CHEN J, WANG M, LI S P, et al. Choice behavior of passenger transfer route for urban rail transit network[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 235-241.)
[2] 石俊刚, 周峰, 朱炜, 等. 基于 AFC 数据的城轨乘客出行路径选择比例估计方法[J]. 东南大学学报(自然科学版), 2015, 45(1): 184-188. (SHI J G, ZHOU F, ZHU W, et al. Estimation method of passenger route choice proportion in urban rail transit based on AFC data[J]. Journal of Southeast University (Natural Science Edition), 2015, 45 (1): 184-188.)
[3] YANSHUO S, PAUL M, SCHONFELDY. Schedule-Based Rail Transit Path-Choice Estimation using Automatic Fare Collection Data[J]. Journal of Transportation Engineering,2015. ( ISSN:0733-947X)
[4] HAMDOUCH Y, HO H W, SUMALEE A, et al. Schedule-based Transit Assignment Model with Vehicle Capacity and seat availability[J]. Transport Research Part B. 2011,45(10):1085-1830. (ISSN: 0191-2615)
[5] 杨东赤, 任华玲, 四兵锋, 等. 基于时刻表的轨道交通网络动态配流模型研究[J]. 系统工程理论与实践, 2015, 35(5): 1214-1223. (YAN D C, REN H L, SI B F, et al. Research on schedule-based dynamic traffic assignment model for rail transit networks[J]. System EngineeringTheory&Practice,2015,35(5):1214-1223.)
[6] 兰珊珊. 基于 AFC 数据的城轨路网客流分析算法研究[D].北京交通大学,2019. Lan S S. Research on passenger flow analysis algorithms of urban rail network based on AFC data[D]. Beijing Jiaotong University. 2019.
[7] 尹浩东. 运营中断条件下城市轨道交通乘客出行行为建模与客流诱导优化研究[D].北京交通大学,2017. YIN H D. Modeling passenger travel behavior and guidance optimization for disruption management in the urban rail transit network[D]. Beijing Jiaotong University. 2017.
[8] 楼哲妮. 基于动态客流的城市轨道交通列车开行方案优化研究[D].北京交通大学,2016. LOU Z N. An optimization research for train plan of urban rail transit based on dynamic passenger flow[D]. Beijing Jiaotong University. 2016.
[9] 李贺. 城市轨道交通网络动态客流计算方法及实证研究[D].北京交通大学,2019. LI H. Urban rail transit network dynamic passenger flow calculation method and empirical study[D]. Beijing Jiaotong University. 2019.
转载请注明来自:http://www.lunwencheng.com/lunwen/dzi/21590.html