摘要:基于传声器阵列测量的波束形成声源识别技术广泛应用于军事、工业、环境等领域。围绕“空间分辨能力增强、寄生虚假声源抑制、定位定量精度提升、鲁棒稳健性能强化、声源识别功能完善”的目标,国内外学者开展了大量研究工作并取得了丰硕成果,反卷积波束形成、函数型波束形成和压缩波束形成三类典型高性能方法先后被提出。为帮助国内学者全面了解三类高性能波束形成方法并加以推广应用,系统阐述其核心思想,全面综述其重要研究进展,根据需要计算的阵列点传播函数的数目对反卷积波束形成进行科学分类,根据采用的网格点类型对压缩波束形成进行科学分类。综述同时涵盖适宜识别阵列前方局部区域内声源的平面传声器阵列和适宜 360°全景识别声源的球面传声器阵列。
关键词:声源识别;反卷积波束形成;函数型波束形成;压缩波束形成;平面传声器阵列;球面传声器阵列
0 前言
波束形成声源识别技术[1-5]利用一组传声器构成的阵列测量声压信号,基于特定波束形成方法后处理测得的声压信号来获取被测对象表面的声学成像图,通过匹配光学照片等方式来直观指示声源,又名“声学照相机”[6],具有测量速度快、因适宜中远距离测量而易于布置等优势[7],在噪声源识别、目标探测、故障诊断等领域被广泛应用,自诞生至今一直备受关注。术语“波束形成”起先是指通过数学转向聚焦方式实现空间指向性的传感器阵列信号处理方法。近年来在声源识别领域,波束形成概 念被大幅外延,早期的定义已不能包罗所有方法。就作者看来,所有适宜阵列中远距离测量且以目标识别为目的的方法都可统称为波束形成,其与近场声全息的本质区别在于后者需近场测量且更适宜于声场重建。
传声器阵列的结构形式决定波束形成声源识别的空间范围和应用场景。平面和球面是最常用的传声器阵列结构形式。平面传声器阵列的所有传声器共平面,几何形状有矩形网格形、圆环形、螺旋形、 Fibonacci 形、扇形轮形等;球面传声器阵列的所有传声器共球面,几何形状有开口球和刚性球。平面传声器阵列适宜识别阵列前方局部区域内声源,典型应用场景包括发动机噪声源识别[8-9]、道路及轨道车辆通过噪声源识别[10-14]、飞机飞越噪声源识别[15-16]等。凭借旋转对称性好和声场记录全面,球面传声器阵列能 360°全景识别声源,适宜在舱室等封闭环境内使用,典型应用场景包括飞机、潜艇、汽车及高速列车舱内噪声源识别[17-20]等。本文同时涵盖平面和球面传声器阵列。
传声器阵列测量声压信号的后处理方法决定波束形成声源识别的性能。延迟求和(Delay and sum, DAS)[21-24]和球谐函数波束形成(Spherical harmonics beamforming, SHB)[25-30]是常用的传统方法。平面传声器阵列采用 DAS;球面传声器阵列理论上既可采用 DAS 又可采用 SHB,实际上主要采用 SHB(低频表现更佳)。两种方法均离散目标声源区域形成一组聚焦网格点,聚焦各网格点时,DAS 根据聚焦点位置或方向对各传声器测量的声压信号进行“相位对齐”和“求和运算”,SHB 根据聚焦点位置或方向对传声器测量声压信号的各阶次球傅里叶变换系数进行“模态强度及球谐函数缩放”和“求和运算”,基于“一组复数加和的模在各复数同相位时最大” 的原理和球谐函数的正交性[31],二者均能在声源位置或方向输出极大值。这些极大值虽能指示声源,但与非声源位置或方向处的输出值差异不显著,最终导致围绕声源位置或方向形成具有一定宽度的 “主瓣”且在其他位置或方向形成高水平的“旁瓣”,主瓣宽度影响空间分辨能力,旁瓣形成寄生虚假声源,使结果分析承受不确定性,故 DAS 和 SHB 均可看作低性能方法。突破 DAS 和 SHB 的性能局限、发展高性能方法对提高声源识别精度和完善声源识别功能具有重要意义。自波束形成技术诞生至今,对高性能声源识别方法的探索从未间断且方兴未艾,包括本文作者在内的大批国内外学者都致力于该主题的研究并取得丰硕成果。反卷积波束形成、函数型波束形成和压缩波束形成三类具有旺盛生命力的高性能方法已被提出。
本文对上述三类高性能方法进行详细综述,旨在帮助国内学者全面系统地了解这些方法。2019 年前,CHIARIOTTI 等[3]亦发表了关于波束形成声源识别技术的综述。本文与文献[3]的主要区别在于: ① 本文基于大量文献对反卷积波束形成进行科学分类并详细介绍每一类的研究进展,文献[3]仅描述部分文献的研究工作;② 本文对压缩波束形成进行系统全面的综述,文献[3]未做此工作;③ 针对球面传声器阵列的三类高性能方法,文献[3]涉及内容较少,本文内容更丰富;④ 文献[3]对波束形成技术的历史、原始物理模型、传声器阵列设计方法、瑞利限及最大旁瓣水平等物理概念进行了详细介绍,本文未重复;⑤ 文献[3]亦对自适应波束形成、正交波束形成等其它高性能方法进行了详细介绍,由于文献[3]之后这些方法的研究进展极少,故本文未重复阐述。对第④和第⑤条涉及内容感兴趣的读者可阅读文献[3]。
1 反卷积波束形成
反卷积波束形成本质上是对传统波束形成的结果进行主瓣宽度缩减和旁瓣污染衰减。从数学角度,反卷积波束形成可统一为求解式(1)所示线性方程组的逆问题
b Aq = (1)
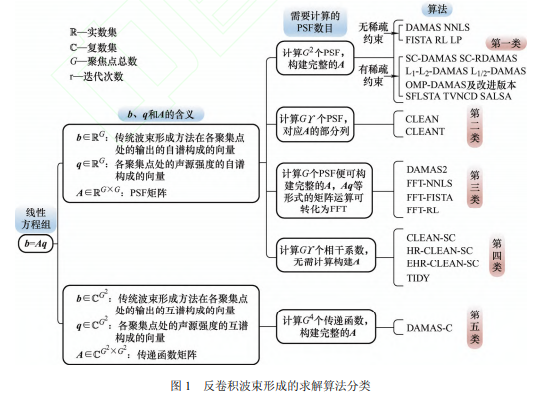
式中,矢量 b 和矩阵 A 已知,矢量 q 未知。求解该线性方程组可从 b 中剔除 A 的影响,重构 q。如图 1 所示,已有求解算法可大致分为五类。前四类中,b 由传统波束形成方法在各聚焦点处的输出的自谱构成,q 由各聚焦点处的声源强度的自谱构成, A 为点传播函数 (Point spread function, PSF)矩阵。PSF 被定义为传统波束形成方法对单位强度单极子点声源的响应,传声器离散采样等因素使 PSF 不为理想 δ 函数是传统方法承受宽主瓣和高旁瓣缺陷的根本原因。第一类算法在每个聚焦点处假设一个声源,计算各声源到各聚焦点的 PSF 构建完整的 A 后迭代求解式(1)。根据迭代过程中对 q 施加的约束,第一类算法又可分为两小类:第一小类只施加元素非负约束,已有算法包括采用高斯-塞德尔迭代方案的反卷积声源成像 (Deconvolution approach for the mapping of acoustic sources, DAMAS)、采用梯度投影法的非负最小二乘(Non-negative least-squares, NNLS) 和快速迭代收缩阈值算法 (Fast iterative shrinkage-thresholding algorithm, FISTA)、采用概率统计法的 Richardson-Lucy (RL)和采用单纯形法的线性规划(Linear programming, LP);第二小类既施加元素非负约束又施加稀疏约束,已有算法包括稀疏约束 DAMAS (Sparsity constrained DAMAS, SC-DAMAS)、稀疏约束稳健 DAMAS (Sparsity constrained robust DAMAS, SC-RDAMAS)、基于弹性网正则化采用 1 A 和 2 A 范数的 DAMAS (L1-L2- DAMAS)、采用 1 2 A 范数的 DAMAS (L1/2-DAMAS)、正交匹配追踪 DAMAS (Orthogonal matching pursuit DAMAS, OMP-DAMAS)及改进版本、光滑 FISTA (Smoothing FISTA, SFISTA)、全变差范数约束反卷积(Total variation norm constrained deconvolution, TVNCD) 和分裂增广拉格朗日收缩算法 (Split augmented lagrangian shrinkage algorithm, SALSA)。增加稀疏约束可加快收敛速度进而带来更清晰直观的成像图,但以引入参数(例如,声源数目、规则化参数、光滑参数等)的恰当选择为前提。第二类算法仅计算构建 A 的部分列,迭代求解式(1)的思路为:用 b 的最大值指示一个声源;计算该声源到各聚焦点的 PSF,即 A 中一列,用其与该声源的强度的乘积表示该声源对 b 的贡献,从 b 中移除该贡献得新 b;重复前两步直至迭代终止,根据每次迭代确定的声源可得 q。已有算法包括应用于频域的清除法 (CLEAN)和其在时域下的变体 CLEANT。第三类算法假设 PSF 空间转移不变(只取决于聚焦点与声源间的相对位置或方向,而与具体位置或方向无关),仅计算中心聚焦点处声源到各聚焦点的 PSF 再结合边界条件便可构建完整的 A,迭代求解式(1)时,诸如 Aq 等形式的矩阵运算还可转化为快速傅里叶变换(Fast Fourier transform, FFT)进行求解。已有算法包括 DAMAS2、FFT-NNLS、FFT-FISTA 和 FFT-RL, DAMAS2 采用雅可比迭代方案,FFT-NNLS、 FFT-FISTA 和 FFT-RL 分别为 NNLS、FISTA 和 RL 的变体。第四类算法求解式(1)的迭代思路与第二类算法类同,不同之处在于第二步:第四类算法用相干系数与传统波束形成方法的输出的乘积表示声源对 b 的贡献。因此,A 完全无需被计算构建,取而代之的是计算传统波束形成方法在各聚焦点处的输出与最大输出间的相干系数。已有算法包括应用于频域的基于源相干性的清除法(CLEAN based on source coherence, CLEAN-SC)、高分辨率 CLEANSC (High-resolution CLEAN-SC, HR-CLEAN-SC)、增强型 HR-CLEAN-SC (Enhanced HR-CLEAN-SC, EHR-CLEAN-SC)及 CLEAN-SC 在时域下的变体 TIDY。第五类中,b 由传统波束形成方法在各聚焦点处的输出的互谱构成,q 由各聚焦点处的声源强度的互谱构成,A 为传递函数矩阵。已有算法命名为 DAMAS-C,其计算构建出完整的 A 后通过施加约束和采用高斯-塞德尔迭代方案求解式(1)。记 R 为实数集,C 为复数集,G 为聚焦点总数,ϒ 为迭代次数,根据上述分析,前四类算法中, G b∈ R 、 G q∈R 且 G G× A∈ R ,第五类算法中, 2 G b∈C 、 2 G q ∈C 且 2 2 G G× A∈ R ,第一类算法需计算 2 G 个 PSF,第二类算法需计算Gϒ 个 PSF,第三类算法仅需计算G 个 PSF,第四类算法不计算 PSF 但需计算 Gϒ 个相干系数,第五类算法不计算 PSF 但需计算 4 G 个传递函数,故可认为上述分类的依据是需要计算的 PSF 的数目。
实际应用中,式(1)中的“=”不绝对成立,b 和 Aq 间的差异越小,重构的 q 越准确。若不考虑测量噪声干扰,第一、二和四类算法中,当且仅当声源互不相干且采用足够多数据快拍来计算传声器测量声压信号的互谱矩阵时,b Aq = 才成立;第三类算法中,使b Aq = 成立不仅需要第一、二和四类算法对应的条件而且需要 PSF 空间转移不变;第五类算法无条件限制。这意味着第一至四类算法最适宜应用于声源互不相干且数据快拍充足的工况,声源间存在相干性及数据快拍缺乏都会降低这些算法的性能,真实 PSF 的空间转移变化还会进一步降低第三类算法的性能;第五类算法则完美适用于任意相干程度声源和任意数据快拍数目。然而,由于涉及超大维度矩阵运算,第五类算法耗时极其严重,这极大地限制了其在实际工程中的推广应用。接下来,第 1.1、1.2 节将分别详细综述上述反卷积算法在平面和球面传声器阵列框架下的研究现状。
1.1 平面传声器阵列
平面传声器阵列框架下,图 1 中涉及算法均已被建立。DAMAS 和 DAMAS-C 均由美国宇航局的 BROOKS 等[32-34]于 2004-2006 年提出。DAMAS2 由美国 OptiNav 公司的 DOUGHERTY[35]于 2005 年提出。 NNLS[36] 和 RL[37-38] 由德国宇航中心的 EHRENFRIED 等[39]于 2007 年引入到传声器阵列声源识别领域并给出相应变体 FFT-NNLS 和 FFT-RL。 CLEAN 最早出现在天文学领域[40-41],由荷兰国家航天实验室的 SIJTSMA[42]于 2007 年引入到传声器阵列声源识别领域并同时提出 CLEAN-SC ; CLEAN-SC在时域下的变体TIDY由DOUGHERTY 等[43]于 2009 年提出;CLEAN 在时域下的变体 CLEANT 由 COUSSON 等[44]于 2018 年提出;2016 —2019 年,SIJTSMA 等[45-48]还相继提出 CLEAN-SC 的性能增强版本 HR-CLEAN-SC 和 EHR-CLEAN-SC;2018 年,本文作者等[49]重新推导 HR-CLEAN-SC 的理论公式并给出详细直观的实施步骤。SC-DAMAS 由美国佛罗里达大学的 YARDIBI 等[50]于 2007 年提出,基于此,法国高等电力学院的 CHU 等[51]于 2012 年提出 SC-RDAMAS,北京航空航天大学的 LI 等 [52] 于 2014 年提出 L1-L2-DAMAS,清华大学的 BAI 等[53]于 2019 年提出 L1/2-DAMAS。LP 由 DOUGHERTY 等[54]于 2013 年提出。FISTA 最早出现在图像处理领域[55],由丹麦科技大学的 LYLLOFF 等[56]于 2014 年引入到传声器阵列声源识别领域并给出相应变体 FFT-FISTA,基于此,重庆大学的 SHEN 等[57]于 2020 年提出 SFISTA。OMP-DAMAS 由加拿大舍布鲁克大学的 PADOIS 等[58]于 2014 年提出,其改进版本由挪威奥斯陆大学的 BERGH[59]于 2018 年提出。TVNCD 和 SALSA 由褚志刚等[60-61]分别于 2018 和 2019 年提出。
国内外学者亦致力于上述算法的性能改进研究。第一和五类算法的最主要问题是耗时严重,尤其第五类。上海交通大学的 MA 等[62-63]采用压缩计算网格提高 DAMAS 的计算效率;浙江大学的 CHU 等[64]用小维度矩阵的卷积近似第一类算法中大维度矩阵的乘积,并采用 GPU 平台进一步加速;合肥工业大学的徐亮等[65]抛弃 DAMAS-C 的互谱表示,令 G b∈C 为单快拍下传统波束形成方法在各聚焦点处的输出构成的矢量, G q∈C 为单快拍下各聚焦点处的声源强度构成的矢量, G G× A∈ C 为从 q 到 b 的传递函数矩阵,提出的方法远快于 DAMAS-C 又可识别相干声源;美国宇航局的 BAHR 等[66-67]采用波空间法提高 DAMAS-C 的计算效率。第三类算法的最主要问题是主瓣宽度缩减及旁瓣水平衰减效果欠佳且仅适用于声源覆盖区域不大的情况,这主要与 PSF 不满足空间转移不变假设有关,采用的边界条件亦有影响。为解决这些问题,EHRENFRIED 等[39] 将 DAMAS2 和 FFT-NNLS 嵌套到考虑 PSF 空间转移变化的迭代运算中,提出嵌套反卷积;美国波音公司的 SUZUKI[68]通过将 PSF 展开为泰勒级数并保留到第二阶引入弱变 PSF,提出采用弱变 PSF 的 DAMAS2 ;DOUGHERTY[35]、丹麦科技大学的 XENAKI 等[69-70]及本文作者[71-72]均通过生成新型聚焦点分布来提高 PSF 的空间转移不变性,前两者生成的聚焦点分布在一组同心球面上,适宜阵列前方三维区域内的声源识别,后者生成的聚焦点分布在同一平面上,适宜阵列前方二维平面内的声源识别; SHEN 等[73-74]尝试用周期边界条件替代习惯采用的零边界条件。四种方法中,前两种能缓解上述问题,但牺牲第三类算法的效率优势,尤其是嵌套反卷积,其计算耗时几乎与第一类算法相当;第三种能缓解上述问题,同时能保留第三类算法的效率优势;第四种能一定程度上提高计算效率,对上述问题的缓解效果不明显。此外,国内外学者还致力于反卷积波束形成在特定场景下的应用研究,例如,移动声源识别[75]、旋转声源识别[76-78]、多运动模式声源识别[79-80]、存在地面反射时的声源识别[81]和水下声源识别[82]。
历经十余年发展,平面传声器阵列的反卷积波束形成技术日趋成熟,已被成功应用于解决发动机[83-85]、汽车[86-89]、飞机[90-91]、高速列车[92]、风力涡轮机[93-94]等对象的噪声源识别问题。反卷积算法种类众多,了解各算法的优缺点才能根据实际需求做出恰当选择,这就需要全面系统地对比分析已有算法的性能。国内外学者已致力于该工作: EHRENFRIED 等[39]对比 DAMAS、DAMAS2、 FFT-NNLS 和 FFT-RL 的性能;YARDIBI 等[95]对比 DAMAS、SC-DAMAS、CLEAN-SC 和协方差矩阵拟 合 [50] 的性能;本文作者 [96] 对 比 DAMAS 、 DAMAS2 、 NNLS 、 FFT-NNLS 、 CLEAN 和 CLEAN-SC 的性能;RAMACHANDRAN 等[97]对比 DAMAS、LP、CLEAN-SC和TIDY的性能;HEROLD 等[98-99]既将 DAMAS、CLEAN-SC、协方差矩阵拟合和正交波束形成[100]进行对比,又将 DAMAS、 NNLS 和 OMP-DAMAS 进行对比。
1.2 球面传声器阵列
球面传声器阵列框架下,图 1 中涉及算法已被部分建立。虽然平面传声器阵列的 DAS 和反卷积算法可移植至球面传声器阵列,例如文献[101],但基于 SHB 为球面传声器阵列发展反卷积更有意义,这是因为 SHB 的低频表现优于 DAS,以 SHB 为基础更利于低频声源的准确识别。本文作者一直致力于此项研究,先后发表了文献[102-106]。2015 年,文献[102]推导 SHB 的 PSF,成功改编第一类算法中的 DAMAS、NNLS 和 RL 及第二类算法中的 CLEAN 使之适用于球面传声器阵列测量,该工作受启发于丹麦科技大学的 TIANA-ROIG 等[107]的一项研究(基于圆谐函数波束形成[108]为安装在刚性球赤道上的圆环形传声器阵列发展 DAMAS2、FFT-NNLS 和 FFT-RL)。为提高计算效率,2016 年,文献[103]又提出适用于球面传声器阵列测量的第三类反卷积并对比不同边界条件的影响。为避免计算 PSF 与真实 PSF 不一致带来的影响,2018—2019 年,文献[104] 推导 SHB 在不同位置输出间的相干系数,文献[105] 推导基于 SHB 的输出确定声源标示点并重构各声源在阵列传声器处产生声压信号的互谱矩阵的相关理论,分别为球面传声器阵列测量实现 CLEAN-SC 和 HR-CLEAN-SC。文献[102-105]未在统一数学框架下实现反卷积,即采用不同 SHB 输出表达式,这不便于应用推广;文献[102-103]计算 PSF 时采用的阶截断方案还不够优化。为解决这些问题,2020 年,文献[106]重新推导 SHB 的输出,将其表示为兼容所有现有反卷积算法的简洁矩阵运算形式,同时优化阶截断方案。除 SHB 外,FAS 方法[109-110]近年来亦被频繁使用,其以 SHB 为基础,相比 SHB 能衰减旁瓣。近期,褚志刚等[111]尝试以 FAS 为基础实现 HR-CLEAN-SC 和 EHR-CLEAN-SC 以期获得更清晰直观准确的结果。
2.1 平面传声器阵列
平面传声器阵列框架下,Dougherty 是函数型波束形成的提出者和倡导者:2014 年,其首次提出该方法[112];同年,其又引入声源密度标准化、脊检测 (Ridge detection, RD)和 LP 来提高该方法的性能[113],声源密度标准化能降低量化偏差,RD 能增强主瓣宽度缩减效果,联合 RD 和 LP 能提高空间分辨能力和声源量化精度;2019 年,其又基于函数型波束形成提出函数型投影波束形成[114],后者用于积分量化前者成像的声源区域,对不相干、部分相干和相干声源均能提供准确结果;2020 年,其又提出低频性能优于函数型投影波束形成的自适应投影波束形成[115] ;同年,其还联合荷兰代尔夫特理工大学的 MERINO-MARTÍNEZ 等[116]对比函数型波束形成、函数型投影波束形成、正交波束形成、CLEAN-SC、 EHR-CLEAN-SC、协方差矩阵拟合、广义逆波束形成[117-118]等方法的性能。除 Dougherty 外,其他国内外学者亦做出许多研究:MERINO-MARTÍNEZ 等[119] 和美国伊利诺伊理工大学的 RAMACHANDRAN 等[120]分别研究函数型波束形成在飞机和风力涡轮机噪声源识别中的应用;本文作者研究声源未落在聚焦点上和传声器及测试通道频响特性幅相误差对函数型波束形成性能的影响规律及机理[121] ;MA 等[122] 基于函数型波束形成提出一种压缩计算网格生成方法用以提高 DAMAS 的计算效率;重庆大学的 XU 等[123-128]将函数型波束形成的思想应用于等效源近场声全息和广义逆波束形成。
2.2 球面传声器阵列
球面传声器阵列框架下,相关研究工作主要由本文作者完成,先后发表文献[129-130]。以球面传声器阵列的常用传统方法 SHB 为基础无法实现函数型波束形成,鉴于此,2015 年,文献[129]在球谐函数域为球面传声器阵列测量建立一种全新方法并以此为基础发展函数型波束形成。2016 年,文献[130] 引入 RD 和 DAMAS 来提高空间分辨能力和量化精度。
3.2 球面传声器阵列
球面传声器阵列框架下,定网格在网、定网格离网和无网格压缩波束形成均已被研究,而关于动网格压缩波束形成迄今尚未见报道。
(1) 定网格在网和离网压缩波束形成。关于定网格在网压缩波束形成,国内外学者已做出较多工作。丹麦科技大学的 FERNANDEZ-GRANDE 等[182-183]推导 D 的表达式、建立 ★ P 的数学模型并基于 1 A 范数最小化进行求解。上海大学的 HUANG 等[184]基于稀疏贝叶斯学习提出一种适用于球面阵列的实值方法。重庆大学的 PING 等[185-186]对比正交匹配追踪、广义正交匹配追踪、 1 A 范数最小化和迭代重加权 1 A 范数最小化四种算法的性能,还基于稀疏贝叶斯学习实现球面传声器阵列的三维声源定位。重庆大学的 YIN 等[187]提出基于自适应重加权同伦算法的压缩波束形成,相比基于 1 A 范数最小化和基于迭代重加权 1 A 范数最小化的压缩波束形成,其具有无需估计噪声、对低信噪比工况适应性好、弱源量化精度高和计算速度快等优势。关于定网格离网压缩波束形成,已有工作尚比较缺乏,目前仅见 HUANG 等[188-189]的两篇报道,其借鉴文献[149] 的思路。
(2) 无网格压缩波束形成。关于无网格压缩波束形成,国内外学者亦做出一些工作。以色列理工大学的 BENDORY 等[190-192]将文献[161-162]中的无网格方法拓展至球面阵列的二维问题,应用于声源识别时,该方法用声源强度的原子范数量度声源分布稀疏性,基于 ANM 建立传声器测量声压信号按模态强度缩放的球傅里叶变换系数的去噪声数学模型,在对偶域采用半正定规划求解该数学模型,基于多项式求根从对偶变量的最优解中提取声源信息。与 BENDORY 等的思路不同,扬州大学的 PAN 等[193-195]为球面阵列发展另一种无网格方法,应用于声源识别时,该方法用声源在传声器处产生声压信号的变换形式的原子范数来量度声源分布稀疏性,基于 ANM 建立传声器测量声压信号的球傅里叶变换系数(或变换系数的协方差矩阵)的去噪声数学模型,在原始域采用半正定规划求解该数学模型,基于球面旋转不变信号参数估计(Estimation of signal parameters via rotational invariance technique, ESPRIT)方法[196]从半正定规划结果中提取声源信息。本文作者亦研究该主题,发表文献[197]。文献[197]中方法的思路与文献[193-195]中方法的思路相似,不同之处在于前者:① 直接建立传声器测量声压信号的去噪声数学模型,丢弃了传声器采样球谐函数需满足正交性的约束条件,有利于高频声源的准确识别;② 为半正定规划的求解发展基于 ADMM 的高效求解器;③ 基于采用三种球谐函数递归关系的新版本球面 ESPRIT 方法[198-200]提取声源信息,能克服旧版本球面 ESPRIT 方法(文献[193-195]中采用)的歧义和奇异问题。
4 结论
传统波束形成声源识别方法围绕声源位置或方向输出的宽主瓣限制空间分辨能力、在其它非声源位置或方向输出的高旁瓣形成寄生虚假声源,导致声源识别结果的分析承受不确定性。围绕“空间分辨能力增强、寄生虚假声源抑制、定位定量精度提升、鲁棒稳健性能强化、声源识别功能完善”的目标,国内外众多学者开展高性能波束形成声源识别方法研究并取得了丰硕成果,新方法、新理论、新算法层出不穷。本文概述了平面传声器阵列和球面传声器阵列的反卷积波束形成、函数型波束形成和压缩波束形成三类高性能方法的核心思想和重要研究进展。根据需要计算阵列 PSF 的数目对反卷积波束形成进行了科学分类,根据采用的网格点类型对压缩波束形成进行了科学分类。作者希望通过这篇综述能够让读者更全面地了解波束形成声源识别领域的最新研究成果并加以推广应用。
虽然近年来针对高性能波束形成声源识别方法国内外学者已作出大量研究工作并取得重要进展,但仍存在一些难题有待解决,需进一步探索。未来值得研究的主题包括:① 强混响环境下高性能波束形成声源识别方法的探索。已有研究多采用自由场假设,测试环境中的混响干扰会劣化声源识别性能,研究在强混响干扰环境中仍能高精度识别声源的波束形成方法有助于扩大波束形成技术的应用空间; ② 三维高性能波束形成声源识别方法的探索。已有研究多关注二维声源识别问题,很少考虑声源深度信息,用已有方法沿深度方向识别声源时,空间分辨能力弱,探索同时在三个维度上均能高精度识别声源的方法对三维空间内声源的准确识别具有重要意义;③ 深度学习与波束形成技术的融合探索。深度学习是机器学习的一个新兴研究方向,能够让机器具有人一样的学习分析能力,将深度学习与波束形成技术相融合以提升声源识别性能及声源识别技术的应用智能化。——论文作者:杨 洋 1, 2 褚志刚 1
参 考 文 献
[1] JOHNSON D H , DUDGEON D E. Array signal processing:Concepts and techniques[M]. New Jersey: Prentice Hall,1993.
[2] VAN TREES H L. Detection,estimation,and modulation theory,Part IV:Optimum array processing[M]. New York:John Wiley & Sons Inc.,2002.
[3] CHIARIOTTI P,MARTARELLI M,CASTELLINI P. Acoustic beamforming for noise source localization: Reviews,methodology and applications[J]. Mechanical Systems and Signal Processing,2019,120:422-448.
[4] MERINO-MARTINEZ R,SIJTSMA P,SNELLEN M, et al. A review of acoustic imaging methods using phased microphone arrays[J]. CEAS Aeronautical Journal,2019, 10:197-230.
[5] GINN K B,HADDAD K. Noise source identification techniques: Simple to advanced applications[C]// Proceedings of the Acoustics 2012 Nantes Conference, 23-27 April 2012,Nantes,France. Hal-00810618,2012: 1781-1786.
[6] MICHEL U. History of acoustic beamforming[C]// Proceedings on CD of the 1st Berlin Beamforming Conference,21-22 November 2006,Berlin,Germany. BeBeC-2006-01.
[7] 褚志刚,杨洋,倪计民,等. 波束形成声源识别技术研究进展[J]. 声学技术,2013,32(5):430-435. CHU Zhigang,YANG Yang,NI Jimin,et al. Review of beamforming based sound source identification techniques[J]. Technical Acoustics,2013,32(5):430-435.
[8] GUIDATI S. Advanced beamforming techniques in vehicle acoustic[C/CD]// Proceedings on CD of the 3rd Berlin Beamforming Conference,24-25 February 2010, Berlin,Germany. BeBeC-2010-04.
[9] 杨洋,倪计民,褚志刚,等. 基于互谱成像函数波束形成的发动机噪声源识别[J]. 内燃机工程,2012,33(3): 82-87. YANG Yang,NI Jimin,CHU Zhigang,et al. Engine noise source identification based on cross-spectra imaging function beam-forming[J]. Chinese Internal Combustion Engine Engineering,2012,33(3):82-87.
[10] 王子腾,杨殿阁,李兵,等. 运动汽车噪声的可视化测量方法比较研究[J]. 振动工程学报,2011,24(5): 578-584. WANG Ziteng , YANG Diange , LI Bing , et al. Comparative study of methods for moving vehicles noise measurement and visualization[J]. Journal of Vibration Engineering,2011,24(5):578-584.
[11] 褚志刚,杨洋,王卫东,等. 基于波束形成方法的货车车外加速噪声声源识别[J]. 振动与冲击,2012,31(7): 66-70. CHU Zhigang,YANG Yang,WANG Weidong,et al. Identification of truck noise sources under passby condition based on wave beamforming method[J]. Journal of Vibration and Shock,2012,31(7):66-70.
[12] GADE S,HALD J,GOMES J,et al. Recent advances in moving-source beamforming[J]. Sound and Vibration, 2015,49(4):8-14.
[13] BALLESTEROS J A,SARRADJ E,FERNANDEZ M D, et al. Noise source identification with beamforming in the pass-by of a car[J]. Applied Acoustics,2015,93:106-119.
[14] ZHANG J,SQUICCIARINI G,THOMPSON D J. Implications of the directivity of railway noise sources for their quantification using conventional beamforming[J]. Journal of Sound and Vibration,2019,459:114841.
转载请注明来自:http://www.lunwencheng.com/lunwen/dzi/21599.html