摘要:以多个虚拟同步发电机(virtual synchronous generator, VSG)控制的电压源型换流站接入交流系统为研究对象,建立含多个 VSG 的闭环系统线性化互联模型,分析多个 VSG 接入对电力系统机电振荡模式的影响,包括 VSG 接入对发电机机电振荡模式的影响和VSG接入对另一个VSG机电振荡模式的影响。采用阻尼转矩分析法揭示多个 VSG 接入对电力系统机电振荡模式的影响机理,并进行理论验证,得出:当 VSG 控制子系统的开环模式与交流子系统的机电振荡模式或者与另一个 VSG 控制子系统的开环模式接近时,子系统间将产生强动态交互过程,导致闭环模式相互排斥,降低系统机电振荡模式的阻尼甚至引发机电振荡。最后,对多个 VSG 接入的交流系统进行非线性仿真,验证上述结论,给出参数设定建议。
关键词:虚拟同步发电机;电压源型换流站;阻尼转矩分析法;机电振荡
0 引言
近年来,随着可再生能源的大力开发和新能源电力系统的快速发展[1],以矢量控制为代表的电压源型换流站得到广泛应用[2-3],由其构成的柔性直流输电(voltage source converter based HVDC, VSC-HVDC)系统成为解决远距离电能传输的有效方案[4]。但是,矢量控制换流站不具有旋转惯性[5],易引入谐波[6],无法为交流系统提供必要的电压和频率支撑,降低电网运行的稳定性[7]。为此,模拟同步发电机的运行特性,提出虚拟同步发电机 (virtual synchronous generator,VSG)控制,增加系统惯性,提供电压和频率支撑[8-11],引起众多学者的广泛关注。
目前针对 VSG 的研究主要分为两个方面:第一方面是 VSG 接入交流系统后,自身控制策略的优化及其控制参数的选择。例如文献[12]基于小干扰线性化模型,通过对比传统无惯性下垂控制和 VSG 控制对系统惯性影响的差异,提出基于 VSG 的下垂控制,结合上述两种控制方式的优势,并用时域仿真法进行验证。文献[13]基于单 VSG 无穷大系统的线性化模型,设计新的解耦控制算法,实现 VSG 有功和无功的独立输出;进一步地,文献[14] 采用小信号分析法深入研究解耦控制算法的参数设计,提出考虑系统稳定性裕量的参数设计方案,基于实物仿真验证方案的有效性。当多个 VSG 同时接入后,传统的 VSG 控制可能引发系统内功率振荡[15],所以文献[15]采用模式分析法,通过调整虚拟定子电抗,提出 VSG 间暂态有功功率的优化分配方法,实现多个 VSG 间的协调控制;类似地,文献[16]考虑到 VSG 输出阻抗、线路阻抗和容量不匹配导致的无功输出偏差,采用模式分析法提出基于虚拟电容的无功分配策略,并在两馈入 VSG 实物系统中验证上述策略可以提升交流电压控制的准确性。
第二方面是 VSG 接入对交流系统稳定性的影响。例如文献[17]建立 VSG 的小信号分析模型,分析控制参数对交流系统稳定性的影响,提出控制参数的优化方案,对实际参数配置有一定的指导意义。文献[18]针对 VSG 控制与发电机间产生的谐振现象,采用频域法分析其对系统频率稳定性的影响,提出基于一阶控制环节的解决措施。文献[19] 基于实物仿真,在原控制基础上提出一种新的阻尼控制方法,有效提升低频振荡的稳定性。对于多个 VSG 接入对系统稳定性的影响研究,目前研究较少,主要集中在控制参数对系统稳定性的影响分析。例如文献[20]采用时域仿真法提出多 VSG 接入后的稳定性评估和参数优化方法,文献[21]则采用模式分析法分析不同的 VSG 控制参数对交流系统振荡模式的影响规律,给出合理的参数选择范围。
综上,单个 VSG 接入对交流系统稳定性的影响研究已经比较广泛,得到频域分析法、模式分析法和实物仿真法等多种方法的验证,并提出多种解决措施。但是对于多个 VSG 接入对交流系统稳定性的影响研究,仍面临以下挑战:
1)目前的稳定性机理研究主要集中在单个 VSG 接入对系统机电振荡模式的影响,在多个 VSG 接入对系统机电振荡模式的影响方面,一般采用模式分析法和时域仿真法,仅针对现象和结果层面进行分析,对应的物理机理解释有待完善。
2)目前提出的参数优化方法和阻尼控制方法虽然可以改善机电振荡模式的阻尼特性,但是较为复杂,仍存在较大的简化空间。
本文研究多个 VSG 接入对交流系统机电振荡模式的影响机理,主要贡献如下:
1)将 VSG 控制子系统和剩余子系统分别单独建模,形成 VSG 控制子系统作为反馈环节,剩余子系统作为前馈环节的线性化闭环互联系统,有利于分析 VSG 控制子系统和剩余子系统间的动态交互过程,降低建模和分析的复杂度。
2)采用阻尼转矩法分析 VSG 控制对系统机电振荡过程的影响机理,发现多 VSG 接入对交流系统机电振荡模式的影响体现在两个方面:一是 VSG 接入对发电机主导的机电模式产生影响,另一则是 VSG接入对另一个VSG的机电振荡模式产生影响。
3)理论证明:当 VSG 控制子系统的开环模式与剩余子系统中任意一个开环模式接近时,子系统间将产生强烈的动态交互过程,导致闭环模式排斥,降低系统机电振荡模式的阻尼,严重地将引发系统机电振荡,从而威胁系统的稳定性。
1 含多个 VSG 的交流系统线性化互联模型
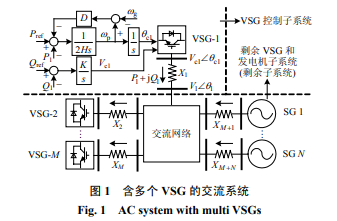
如图 1 所示为含多个 VSG 的多机交流系统,共 有 M 个 VSG 和 N 个发电机 (synchronous generator,SG)。Xi(i = 1,2,⋅⋅⋅, N + M)为 VSG 与交流系统连接线路上的电感,Vi = θ i(i = 1,2,⋅⋅⋅, N + M)为 VSG 与交流系统连接处的节点电压及相角,Vci = θ ci (i = 1,2,⋅⋅⋅, M)为 VSG 输出的电压幅值及相角, Vgi = θgi(i = 1,2,⋅⋅⋅, N)为 SG 输出的电压幅值及相角, Pi + jQi(i = 1,2,⋅⋅⋅, N + M)为 VSG-i 与剩余子系统间的动态交互功率。以图 1 中虚线为分界线,可分别建立 VSG 控制子系统的开环线性化模型和剩余 VSG 和发电机子系统(后简称剩余子系统)的开环线性化模型,考虑到本文的研究对象主要为机电频段,所以忽略系统中的高频动态过程以简化研究。
1.1 VSG 控制子系统的开环线性化模型
VSG 采用文献[22]中的控制策略,如图 1 所示。其中 ωp 为 VSG 等效內电势的频率,ωg 为电网实际频率,ω0 为电网基值频率,Pref、Qref分别为有功和无功的设定值,H 和 D 分别为虚拟同步机的惯性常数与阻尼系数,K 为无功控制器的增益系数。
3 案例验证
3.1 系统介绍
如图 4 所示是 1 个含有 3 台 VSG 和 2 台发电机的交流系统,其中发电机采用文献[23]的模型及其参数,VSG 采用文献[22]的模型及其参数。不失一般性,案例以接入 VSG-3 为研究对象,从 VSG 接入对发电机机电振荡模式的影响和 VSG 接入对另一个 VSG 机电振荡模式的影响两个方面验证:当接入 VSG 的开环模式与系统中原有的开环机电模式重合时,会降低闭环系统机电振荡模式的阻尼,甚至可能引发机电振荡。
在 VSG-3 接入前,计算得到剩余子系统中共有 4 个开环机电模式,根据模式参与性,确定各个模式对应的发电机和 VSG 编号如表 1 第 2 行所示。
3.2 VSG 接入对发电机机电振荡模式的影响
依据 2.2 节中的理论分析,VSG-3 的开环模式应该远离系统中现有的开环模式,以避免强交互的发生。否则,将产生模式排斥,降低系统中机电振荡模式的阻尼,验证如下:
调整 VSG-3 的参数使得其开环模式与发电机机电振荡模式接近,如表 1 第 2 行最后一列所示。然后将 VSG-3 接入,得出系统的闭环振荡模式如表 1 第 3 行所示。
通过对比图 7 中点 B 和点 C 处的非线性仿真结果,可以发现:当 VSG-3 与发电机 1 产生强动态交互过程时,VSG-3 的有功功率产生了较强的功率波动,降低了系统中机电振荡的阻尼,对系统产生了不利影响;当调节参数使得开环模式远离后(点 C),子系统间的动态过程减弱,系统中机电振荡的阻尼有所回升,与图 6 的分析结果一致。
虽然以 VSG-3 的接入为例进行了分析,但上述分析可推广得出以下一般性结论:
1)当接入 VSG 的开环模式与系统中任意发电机的开环模式接近时,子系统间将产生强烈的动态交互作用,导致闭环模式相互排斥,降低了系统机电振荡模式的阻尼,影响了系统在机电频带下的稳定性。
2)考虑到上述现象的本质是由于子系统间开环模式接近造成的,所以可以通过调节 VSG 的控制参数,使得子系统间开环模式相互远离,避免强动态交互过程带来的不利影响。
3.3 VSG 接入对另一个 VSG 机电振荡模式的影响
同理,VSG 与 VSG 之间也会发生强动态交互过程,影响系统机电振荡模式的阻尼,可以通过选取合适的参数进行消除,简要说明如下。
当 VSG-3 的开环控制模式λvsg3与 VSG-1 的开环模式λvsg1接近时,将发生强烈的功率交互现象,并导致 VSG-1 的闭环模式 vsg1 λ ˆ 失稳,如表 2 所示。
此时 VSG-1 和 VSG-3 的状态变量将在 VSG-1 的闭环模式 vsg1 λ ˆ 中呈现较高的参与性,如图 8(a)所示,并可通过调节参数简便地消除:如图 9 中区域 A 所示,调节 VSG-3 的控制参数从 H = 17.35、 D = 8.77 到 H = 20.45、D = 12.23,开环模式λvsg3将从点 D 移至点 C,远离λvsg1。此时模式 vsg1 λ ˆ 的参与 性如图 8(b)所示,VSG-3 和 VSG-1 间的强动态过程得以消除,模式排斥消失,系统恢复稳定。
但是,随着并网 VSG 的增多,VSG 与 VSG 控制模式重合的概率会大大增加,将增大 VSG 间发生强动态交互的风险,说明如下:
如图 9 区域 B 所示,当 VSG-3 的控制参数从 H = 13.55、D = 8.77 调节到 H = 8.15、D = 6.08 时,开环模式λvsg3 将从点 D 移动到点 E,远离了λvsg1,结合图 10(b)的参与性分析结果,可知上述参数调整方式成功消除了与 VSG-1 间的强动态交互过程,使得系统恢复稳定。但是,由于 VSG 数量较多,导致模式分布较为紧密,当 VSG-3 的开环模式位于点 E 时,将与 VSG-2 产生强烈的动态交互过程,并再次导致系统失稳,此时 VSG-2 闭环模式 vsg2 λ ˆ 的参与性如图 10(a)所示。
上述分析充分论证了:当接入的 VSG 数量太多时,将大大增加强交互发生的风险,给参数的设定带来困难。为了避免上述情况,应综合考虑低频段内全部的机电振荡模式,在复平面内合理规划接入 VSG 的模式位置,以避免开环模式相互接近的情况。以本文图 4 的案例为例,可考虑将 VSG-3 的开环模式 λ vsg3 设置于 VSG-2 模式的上方 H = 6.56、D = 5.28(图 9 中点 F),避免与其他机电模式接近。
最后,对点 F 和点 E 处的运行工况进行非线性仿真,验证分析正确性和参数调整的有效性。系统在 0.1s 于节点①处增加 20%的有功负荷,并于 0.2s 时消除,结果如图 11 所示。
4 结论
本文基于含多个 VSG 的交流系统线性化互联模型,采用阻尼转矩法分析了 VSG 接入对系统机电振荡模式的影响机理并进行了论证,给出了参数设定的建议,主要有以下结论:
1)当接入 VSG 的开环模式与系统中任意发电机或者 VSG 的开环模式接近时,可能导致系统中的机电振荡模式发生排斥现象,降低甚至破坏系统在机电频带下的稳定性。
2)上述现象的物理机理解释是:子系统间的开环模式接近时,接入的 VSG 将会给系统提供一个幅值较大的电磁转矩,引起 VSG 与系统间动态交互功率的剧烈波动,影响系统在机电频带下的稳定性。
3)避免强动态交互现象的参数设定建议是:对于单个VSG接入小系统的情况,可调整接入VSG 的控制参数使得其开环模式远离系统中原有的机电振荡模式;对于多 VSG 接入系统的情况,应在复平面内合理安排VSG的模式位置,避免VSG与VSG 间开环模式的重合,消除强交互带来的不利影响。
4)当多个 VSG 接入系统后,发生强交互现象的概率将会上升,针对虚拟同步发电机数量变化对电力系统机电振荡模式影响的定量分析有待于在日后工作中进一步深入探究,是一项具有意义的挑战性工作。——论文作者:付强,杜文娟* ,王海风
参考文献
[1] 陈霞,林卫星,孙海顺,等.基于多端直流输电的风电并网技术[J].电工技术学报,2011,26(7):60-67. Chen Xia,Lin Weixing,Sun Haishun,et al.LCC-MTDC technology for wind farms integration[J].Transactions of China Electrotechnical Society,2011,26(7):60-67(in Chinese).
[2] 徐峥.柔性直流输电系统[M].北京:机械工业出版社, 2014(未找到本条参考文献,请核对). Xu Zheng.Flexible HVDC system[M].Beijing:China Machine Press,2014(in Chinese).
[3] 汤广福.基于电压源换流器的高压直流输电技术[M].北京:中国电力出版社,2010. Tang Guangfu.Voltage source converter based high voltage direct current transmission technology[M] . Beijing:China Electric Power Press,2010(in Chinese).
[4] 王成山,罗凤章,张天宇,等.城市电网智能化关键技术[J].高电压技术,2016,42(7):2017-2027. Wang Chengshan,Luo Fengzhang,Zhang Tianyu,et al. Review on key technologies of smart urban power network[J].High Voltage Engineering,2016,42(7): 2017-2027(in Chinese).
[5] 王炜宇,李勇,曹一家,等.基于虚拟调速器的 MTDC 虚拟同步机控制策略[J].中国电机工程学报,2017: 1-11. WANG Weiyu,Li Yong,Cao Yijia,et al.The virtual synchronous generator technology based on virtual governor for MTDC system[J].Proceedings of the CSEE, 2017:1-11(in Chinese).
[6] 王磊,张琛,李征,等.双馈风电机组的虚拟同步控制及弱网运行特性分析[J].电力系统保护与控制,2017, 45(13):85-90. Wang Lei,Zhang Chen,Li Zheng,et al.Virtual synchronous generator control for DFIG wind turbines and its operation characteristics in weak grid[J].Power System Protection and Control,2017,45(13):85-90(in Chinese).
[7] 吕志鹏,盛万兴,刘海涛,等.虚拟同步机技术在电力系统中的应用与挑战[J].中国电机工程学报,2017, 37(2):349-359. Lü Zhipeng,Sheng Wanxing,Liu Haitao,et al. Application and challenge of virtual synchronous machine technology in power system[J].Proceedings of the CSEE, 2017,37(2):349-359(in Chinese).
[8] 张波,颜湘武,黄毅斌,等.虚拟同步机多机并联稳定控制及其惯量匹配方法[J].电工技术学报,2017, 32(10):42-52. Zhang Bo,Yan Xiangwu,Huang Yibin,et al.Stability control and inertia matching method of multi-parallel virtual synchronous generators[J].Transactions of China Electrotechnical Society , 2017 , 32(10) : 42-52(in Chinese).
[9] 王金华.虚拟同步发电机的同步频率谐振机理和阻尼抑制[D].杭州:浙江大学,2016. Wang Jinhua.Synchronous frequency resonance of virtual synchronous generators and damping control[D] . Hangzhou:Zhejiang University,2016(in Chinese).
[10] 徐海珍,张兴,刘芳,等.基于超前滞后环节虚拟惯性的 VSG 控制策略[J].中国电机工程学报,2017,37(7): 1918-1927. Xu Haizhen,Zhang Xing,Liu Fang,et al.Virtual synchronous generator control strategy based on lead-lag link virtual inertia[J].Proceedings of the CSEE,2017, 37(7):1918-1927(in Chinese).
[11] 李武华,王金华,杨贺雅,等.虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J].中国电机工程学报,2017,37(2):381-391. Li Wuhua,Wang Jinhua,Yang Heya,et al.Power dynamic coupling mechanism and resonance suppression of synchronous frequency for virtual synchronous generators[J].Proceedings of the CSEE,2017,37(2): 381-391(in Chinese).
转载请注明来自:http://www.lunwencheng.com/lunwen/dzi/21702.html