摘 要: 固体蓄热器无论作为热电联产机组( CHP) 的配置系统还是作为清洁电力的消纳系统都起到一定的“削峰填谷”作用。为了提高固体蓄热器的蓄热效率及蓄热容量,首先对工程常用蓄热体结构的蓄热过程提出了一种热物理参数非定值分析方法,并通过实验验证了该数值分析方法的可靠性。对现有蓄热体结构提出截面和功率分布的优化方式,通过建立数值分析方法对优化前后蓄热体结构进行蓄热性能比较,得出截面优化方式和功率分布优化方式在10 h时刻的最高温度分别降低了 3. 6% 和 4. 0% ,在 600 ℃ 目标温度下的蓄热容量分别提高了 5. 0% 和 6. 5% 。结合截面优化和功率分布优化的特点进而提出复合优化方式,该优化方式具有横、纵两个方向的优化效果,与无优化结构的蓄热体相比,在 10 h 时刻的最高温度降低率和 600 ℃目标温度下的蓄热容量提高率分别为 7. 2% 和 11. 0% 。
关 键 词: 固体蓄热器; 蓄热体; 截面优化; 功率分布优化; 复合型优化
引 言
固体蓄热器以电力作为输入,热能作为输出,通过电热转换形成一套热能储存、热能释放的、循环机制[1 - 3]。蓄热体作为固体蓄热器的能量存储介质,其蓄热材料和结构决定着蓄热容量和蓄热终止时刻温度分布的均匀度[4 - 6]。MgO 粉 末挤 压 烧 结 的 MgO 砖是目前热导率、耐高温性及热膨胀性等综合热物理性能较高的储热介质[7 - 9]。针对蓄热体结构的研究中,邢作霞等人[10]通过改变蓄热体整体孔隙率及单双通道结构参数得到综合性能良好的定参数化蓄热体尺寸。胡思科等人[11]以蓄热体作为整体结构,采用数值模拟方法比较了不同数量的圆形和方形蓄热孔对蓄、放热过程的影响,得到蓄热孔蓄热量与达到目标蓄热时间成反比的结论。
目前,对蓄热体结构的研究多侧重于改变整体形状和蓄热孔数量方面,而针对工程常用蓄热体结构的优化研究甚少。本文首先对现有蓄热体结构建立数值分析模型,并进行实验验证; 从蓄热体结构和蓄热功率的角度出发,分别对现有蓄热体提出蓄热孔截面结构优化和加热元件功率分布优化; 结合两种优化形式及优化结果,提出一种复合型蓄热的优化方法,并将蓄热容量、温差缩小率及最高温度降低率等参数指标与现有蓄热体结构进行比较分析。
1 数值模拟与实验验证
1. 1 蓄热体结构及物理模型
工程实际应用的 MgO 砖及蓄热体结构如图 1 所示。采用夹层蓄热式布置,夹层与蓄热层交错排列,保证蓄热体结构受热稳定性,夹 层 中 间 采 用 MgO 砖间隔出放置电加热丝的蓄热孔。
在对物理模型边界条件的处理中,以直接作用到蓄热孔四周壁面的热传导代替蓄热过程中加热元件的热辐射过程,蓄热体内 MgO 砖之间的面接触热阻忽略不计,蓄热体外壁面做绝热处理,热物性做非定值参数处理,最终得到的物理模型如图 2 所示, K1 ~ K4为模拟温度监测点。
1. 2 数值模拟
采用 ANSYS Workbench 中的 Steady-State Thermal 及 Transient Thermal 模块进行热力学分析[12]。首先,将 Solidworks 软件中建立的模型导入 ANSYS Workbench 流程图内,然后进行材料属性及热物理参数处理,根据 MgO 砖比热容、热导率与温度的关系,经二次函数拟合得到 MgO 砖比热容、热导率和温度的拟合公式为:
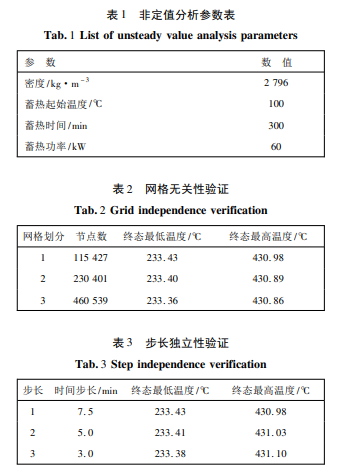
最终得到的数值模拟参数如表 1 所示。进行网格无关性验证和步长独立性验证,网格无关性验证结果如表 2 ~ 表 3 所示。从表中可以看出,网格节点数的增加对终态温度基本无影响,因此网格划分 1 的节点数满足本文的计算精度需求。从表中可以看出,时间步长的等比例缩小对终态温度影响不大,因此本文选取时间步长为7. 5 min。
1. 3 实验验证
蓄热体实验模型如图 3 所示。加热元件为螺距 14 mm、直径 3. 5 mm 的镍铬加热丝,采用 Y 型接法进行连接。保温层采用 150 mm 厚度的纤维棉做保温填充物,50 mm 厚度的硅酸棉板用于外部固定。为了保证对称结构蓄热体不同部位的温度验证,选取 K1,K2,K3,K4 四点作为温度探测点。温度传感器采用铠装型热电偶,量程 0 ~ 1 300 ℃,放置到砖体内深度 50 mm 处,其他相关参数如表 4 所示。
由图 4 中可知,非定值数值分析方法与实验测得的升温趋势是一致的,验证了非定值数值分析方法能够成为进一步研究的可靠依据。
2 蓄热体截面结构优化
由于蓄热体的砖型具有通用性,在不改变砖型的基础上改变蓄热体结构中孔的横向尺寸,分析其对蓄热性能的影响。蓄热孔变参数结构如图 5 所示。由于蓄热体为对称结构,因此可取 1 /4 结构的蓄热孔横向尺寸进行参数化处理。根据蓄热孔热传导区域面积确定 a1、a2、a3 尺寸为方形结构,对 a2、 a3,b2、b3 和 c2、c3 进行等差参数赋值,得到 5 组参数值如表 5 所示。
根据表 5 的数据进行蓄热过程分析,蓄热体到达目标温度的相关参数如表 6 所示。截面优化后的蓄热容量高出等截 面 蓄 热 孔 5. 0% ,蓄 热 体 到 达 10 h的蓄热最大温差为 214. 54 ℃,相比等截面蓄热体温差缩小了 20. 3% ,最高蓄热温度降低了 3. 6% 。
选取综合表现最优的第Ⅲ组蓄热孔截面优化尺寸和无优化的蓄热体结构在蓄热 10 h 时的温度分布云图进行比较,比较结果如图 6 所示。从图中可以看出,蓄热孔的截面优化对横向分布的温度改善较为明显,对纵向的温度分布影响较小。
图 7 为 A - A 截面的仿真温度分布曲线。从截面温度分布可以看出,无优化的 A - A 截面温度呈凸抛物分布,截面温度差值为 54. 76 ℃ ; 而截面优化后的 A - A 截面温度呈波动性恒值分布,截面温度差值为 25. 17 ℃,优化后的截面温度分布更均匀。
3 蓄热功率分布优化
蓄热功率优化分析模型如图 8 所示。从无优化蓄热体纵向温度分布看,在蓄热过程中 P3 所在列及其对称列为最高温度分布区。考虑到蓄热功率优化为单方向性的优化方式,并结合工程中电阻丝的连接形式,决定将 P1,P4 及 P7 所在行的各蓄热孔进行等功率赋值。根据模型的对称性设置 3 个加热功率变量,使用 Workbench 中的 Design Exploration 工具,采用梯度迭代法对蓄热功率进行参数化处理,最终计算结果如图 9 所示。
从图 9 中可以看出,在迭代至第 8 次时出现了蓄热温度极值,将该迭代次数下的蓄热性能参数与无优化结构蓄热性能参数进行对比,对比结果如表7 所示。功率优化后的蓄热体达到目标温度的时长增加了6. 6% ,蓄热容量增加了32. 5 kWh,蓄热体温差缩小了 18. 7% ,最高蓄热温度降低了 4. 0% 。
图 10 为功率优化后蓄热体结构在蓄热 10 h 时刻的温度分布云图。从图中可以看出,蓄热体功率优化后只对纵向的温度分布产生了影响,对横向温度分布影响较小。
图 11 为 B - B 截面的温度分布曲线。可以看出,功率优化后的纵向截面温度分布更均匀,无优化的截面温度差值为 74. 32 ℃,优化后的温度差值为 32. 76 ℃。
4 蓄热过程复合型优化
复合型优化是在结构优化的基础上进行功率优化,选取蓄热体截面优化中第Ⅲ组作为基础模型,采用梯度迭代方式对功率进行赋值优化,如图 12 为优化结果。经过 10 h 的蓄热过程后,进行变截面优化的蓄热体最高温度的最低值为 661. 82 ℃,而复合优化的最低值为 637. 38 ℃,优化率提升了 3. 7% 。
图 12 和图 13 分别为复合优化后蓄热过程温度曲线及终止时刻的温度分布云图。从温度分布图可以看出,在终止时刻的温度分布较为均匀,横、纵方向均有改善。表 8 为 3 种优化方式与无优化结构蓄热体对比结果。可以看出,复合优化方式对蓄热体的蓄热容量、终止时刻的温差和温度分布等方面的性能均有提升。复合优化的加热方式能够在不改变蓄热体结构和提高功率的前提下,将蓄热容量增大 11. 0% ,将蓄热终止时刻的最高温降低 7. 2% ,在优化条件简化的同时达到了较好的优化效果。
5 结 论
( 1) 对于工程常用蓄热体,在热物理参数非定值条件下,建立了一种数值模拟方法,并通过实验验证了该数值模拟方法的可靠性。
( 2) 对现有蓄热体结构提出截面和功率分布优化方式,通过建立的数值模拟方法分析,并与无优化结构的蓄热体相比较,得出两种优化方式在 10 h 时刻的最高温度降低率分别为 3. 6% 和 5. 0% ,600 ℃ 目标温度下的蓄热容量提高率分别为 4. 0% 和 6. 5% 。
( 3) 提出一种结合截面和功率优化的复合优化方式,该优化方式具有横、纵两个方向的优化效果,与无优化结构的蓄热体相比,在 10 h 时刻的最高温度降低 7. 2% ,600 ℃ 目标温度下的蓄热容量提高 11. 0% ,600 ℃目标温度下的温差缩小 37. 8% 。——论文作者:徐耀祖1 ,商向东1 ,徐景久2 ,刘轶菡3
参考文献:
[1] 杨小平,杨晓西,丁 静,等. 太阳能高温热发电蓄热技术研究进展[J]. 热能动力工程,2011,26( 1) : 1 - 6,118. YANG Xiao-ping,YANG Xiao-xi,DING Jing,et al. Research progress of solar thermal power generation and heat storage technology [J]. Journal of Engineering for Thermal Energy and Power,2011, 26( 1) : 1 - 6,118.
[2] 王 艳,白凤武,王志峰. 高温空气在蜂窝陶瓷体内蓄热特性研究[J]. 工程热物理学报,2011,32( 9) : 1541 - 1544. WANG Yan,BAI Feng-wu,WANG Zhi-feng. Study on thermal storage characteristics of high temperature air in honeycomb ceramics[J]. Journal of Engineering Thermal Physics,2011,32 ( 9 ) : 1541 - 1544.
[3] LAING D,LEHMANN D,FIB M,et al. Test results of concrete thermal energy storage for parabolic trough power plants[J]. ASME Journal of Solar Energy Engineering,2009,131 ( 4 ) : 410071 - 410076.
[4] 苏俊林,张亚仁,胡月红. 固体蓄热式电锅炉蓄热模拟及实验[J]. 热能动力工程,2007( 6) : 638 - 641,689. SU Jun-lin,ZHANG Ya-ren,HU Yue-hong. Solid heat storage electric boiler heat storage simulation and experiment[J]. Journal of Engineering for Thermal Energy and Power,2007( 6) : 638 - 641, 689.
[5] 徐耀祖,阿迪力江·对山拜,商向东,等. 基于高倍率蓄热的固体蓄热器研究及应用分析[J]. 热能动力工程,2020,35( 10) : 72 - 78. XU Yao-zu,ADILIJIANG D S B,SHANG Xiang-dong,et al. Research and application analysis of solid heat storage based on high storage[J]. Journal of Engineering for Thermal Energy and Power, 2020,35( 10) : 72 - 78.
转载请注明来自:http://www.lunwencheng.com/lunwen/dzi/21743.html