摘要 针对无位置传感器永磁同步电机控制系统中转子位置与转速无法直接测量的问题,提出基于滑模观测器的转子位置间接检测方法。通过研究低速时滑模观测器的估算误差较大的特点,分析无位置传感器控制方式下电机存在无法零速起动的问题,利用变压变频控制策略进行他控起动。依据滑模观测器的电流跟随特性和滑模控制器的转速跟随特性,同时引入时变项,在提高滑模面收敛速度的基础上实现了调速系统由他控方式向自控方式的平滑过渡。仿真和实验证明,提出的算法不仅解决了滑模观测器在零速及附近的低速范围内所存在的预测死区问题,而且削弱了两种控制方式切换过程中产生的抖振。
关键词:永磁同步电机 无位置传感器 滑模观测器 滑模控制器 变压变频控制
0 引言
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因其良好的控制性能而得到越来越广泛的应用。PMSM 依靠转子位置信号实现转子与定子旋转磁场之间的同步。无位置传感器控制技术采用预测方法获得转子位置,因具有成本低、硬件复杂程度小以及可靠性高的特点而引起了广泛的重视,逐渐成为 PMSM 研究领域内的热点问题[1-11]。
研究内容以转子位置的获取为核心而展开,文献 [1-4] 提出的模型参考自适应系统( Model Reference Adaptive System, MRAS)法基于稳定性理论对永磁同步电机进行转速辨识,状态和速度的渐近收敛性由 Lyapunov 方程和 Popov 超稳定性理论保证。文献[4]针对永磁无刷直流电机的凸极效应构建转子反电动势自适应的定子电流观测器,进而估算出电磁转矩。文献[6-8]通过将滑模观测器技术引入到无位置传感器控制策略中,并分别采用模糊控制方法、分段线性模型和径向基神经网络模型改善滑模观测器的性能。上述方法利用电机的定子电压和电流来计算电机转子的位置,在电机达到满足计算要求的定子电压和电流的速度后均能较好预测永磁同步电机的转子位置而实现电机的无位置传感器控制,但在低速或零速下定子电压和电流通常难以满足预测计算的要求,因而不适合低速或者零速。换言之,上述方法必须解决电机的起动问题后才可以投入应用。
文献[9-11]提出了高频注入的方法,利用电机转子的凸极效应,通过向定子绕组注入三相对称高频旋转电压,检测定子电流来估算转子位置,从而实现无位置传感器控制方式下永磁同步电机的起动。该方法虽然可以应用于较宽的速度范围且低速时也可获得较好的估算结果,但是高频信号的注入会带来高频噪声,增加了系统中的干扰源,可能会造成系统运行过程的不稳定。因此,合理实现无位置传感器永磁同步电机的起动技术,已成为现今亟待解决的问题。
本文采用他控起动和自控运行策略,即在转子定位以后,给电机定子一个旋转磁场使电机起动,起动后滑模观测器不断对电机的电流和转速进行观测,待电机起动到其电流、电压满足预测计算时再切换到自控方式运行。本文利用滑模观测器的电流跟随特性,使得观测电流趋近于实际电流值。针对调速系统中电流相比于转速变化速率较快的特性,在电流观测值等于实际值后,利用滑模控制器的转速跟随特性,实现调速系统由他控模式向自控模式的平滑过渡。本文内容安排如下:首先讨论永磁同步电机无位置传感器控制系统的系统结构和对象模型;然后提出基于滑模观测器的转子位置与转速的估算方法,以及基于滑模控制器的控制方式切换方法,并利用 Lyapunov 稳定性理论对其可行性进行论证;最后给出了仿真分析及原型实验。实验结果证明,本文提出的控制策略具有较高的综合控制性能。
1 PMSM 无位置传感器系统结构及对象模型
1.1 系统结构
PMSM 无位置传感器控制系统框图如图 1 所示。
图 1 中,控制系统主要由滑模控制器(Sliding Mode Controller, SMC)、滑模观测器(Sliding Mode Observer, SMO)、他控模块(Separately Controlled Module, SCM)、切换规则、电流调节器(Automatic Current Regulator, ACR)、Park 变换器、Clarke 变换器、Park 逆变换器(Ipark)、SVPWM 模块、智能功率模块(Intelligent Power Module, IPM)和永磁同步电机等环节组成。其中,SCM 用于实现电机的零速起动;SMO 采集定子电压和电流信号并估算转子位置与转速;SMC 则是在两种控制方式下的输出电流误差趋近于零时,实现系统由他控方式向自控方式的平滑过渡。
3 滑模控制器设计
滑模变结构控制系统的运动轨迹由两部分组成:运动轨迹远离滑模面的趋近运动和运动轨迹位于滑模面附近的滑模运动。滑模控制器的设计分为滑模面的选择和控制律的设计两步。
无位置传感器 PMSM 调速过程主要分为三个步骤:他控起动、自控运行以及由他控方式向自控方式的切换。其中,由他控方式向自控方式的切换过程对应于滑模控制中的趋近运动,而自控运行则对应于滑模控制中的滑模运动。分别对调速过程中的三个步骤进行讨论。
3.1 他控起动
由图 1 可知,当前的 PMSM 无位置传感器控制系统为矢量控制系统。当电机转速位于零速或附近的低速范围内时,无法避免控制死区及观测死区的问题,此时矢量控制系统内的转速环为开环状态。因此,需要采取他控方式在不改变矢量控制系统结构的前提下来实现电机的零速起动或停机。
为保证电机能够平滑起动或停机,即须保证系统产生的定子圆形旋转磁场的幅值与相位能稳定地增大或减小。图 2 给出了起动过程中电压空间矢量的变化规律,图中 α 轴与 β 轴分别代表电压空间矢量在静止两相 αβ 坐标系下的分量;相互嵌套的虚线圆为电压空间矢量在幅值恒定时旋转一周所产生的状态轨迹;U U 1 6 为由逆时针旋转顺序增大的六个电压空间矢量,随着矢量幅值的增大,电机转速也将相应地增大,从而实现电机的平滑起动。
相关知识推荐:传感器应用论文可投稿期刊
然而,在他控方式下,电磁转矩容易受到电网、负载及电机自身各种扰动的影响,从而导致转子转速与定子旋转磁场的同步转速无法保持一致,即电机失步。
4 仿真
本文在应用变压变频控制策略进行 PMSM 他控起动的基础上,加入 SMO 对转子位置与电机转速进行预测,并根据预测结果实时地完成 PMSM 无位置传感器控制系统由他控方式向自控方式的切换。为验证本文提出的算法在电机位于零速附近以及控制方式完成切换过程中的系统响应特性,给出了以斜坡与正弦波信号叠加作为输入的系统仿真结果。
以斜坡与正弦波信号叠加作为输入的系统速度输出响应和跟随误差如图 6 所示,而相应的电机转子预测波形与实测波形对比曲线如图 7 所示,图中纵向虚线标示出了控制方式切换的时间点。不失一般性,仅截取波形中的第一个周期进行分析讨论。从系统速度输出响应与跟随误差曲线可以看出,当系统控制方式为他控方式时,由于此时为转速环开环控制,系统无法针对当前的转速误差给出实时的调整,因此速度输出响应与给定速度之前存在较大的误差;当系统控制方式由他控方式向自控方式切换时,切换过程较为平稳,此时转速所产生的抖振也较小;而当系统控制方式切换为自控方式后,转速环亦随之切换为闭环控制,系统能够针对当前的转速误差进行实时调整,因此此时速度输出响应与给定速度之间的误差非常小。
从电机转子预测波形可以看出,当电机转速在零附近时,转子位置预测波形与实测波形之间存在较大的误差,电机当前运行速度亦无法准确获取,需要将控制方式切换为他控方式实现电机的零速起动或停止;而当转子位置预测波形与实测波形之间的误差逐渐缩小时,电机当前运行速度即可准确计算出来,此时可将控制方式切换为自控方式以保证系统的高性能运行。
5 实验
本文提出的控制策略在 PMSM 伺服系统进行了实验验证,实验平台如图 8 所示。主控板的核心是 DSP 处理器,其具体型号为 TMS320F2812。PC 主要通过采集伺服电动机反馈的数据进行分析比较,编码器则是用于将实际转子位置角度与预测转子预测角度进行对比。实验结果如图 9~图 13 所示。
图 9 给出了 PMSM 无位置传感器控制系统以斜坡与正弦波信号叠加作为输入的输出响应曲线及误差曲线,其中纵向虚线为控制方式切换的时间点,纵坐标为标幺值。当电机刚开始运行时,为在实现他控起动的同时测试系统的跟随性能,设定斜坡信号的斜率略低于正弦波的斜率,受到转速开环控制的影响,转速输出响应无法及时地跟随输入给定波形的变化,二者之间存在着一定的误差;而当电流与转速满足控制方式切换要求后,系统切换为自控方式运行,转速开环控制此时则转变为闭环控制。此时,给定转速发生跳变,驱使转速的输出响应迅速地跟随输入信号的变化,并进而使得系统输出与输入之间的误差能够维持在一个较小的范围内。之 后,若电机转速降低以至于转子位置角的预测精度难以满足自控方式的运行,则再次将系统的控制方式切换为他控方式,此时则将斜坡信号的斜率设定为与正弦波的斜率相等以保证系统的平稳运行。
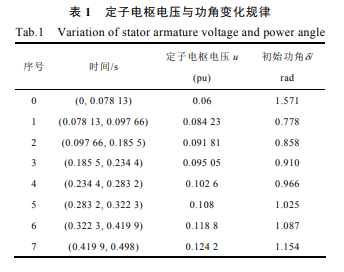
分析图 9 中速度响应曲线的零速起动过程,可得出他控方式下定子电枢电压给定与相应的电机转速变化曲线如图 10 所示。从图 10 中可以看出,根据定子电枢电压取值的不同,可将电机的起动过程分为 8 个阶段。其中,阶段 0 为电机的磁定位过程;在磁定位结束后,由于此时电机转速很低,导致无法准确获取到转子位置角。因此,只能通过调节定子电枢电压与功角的给定值实现电机的他控起动,分别对应于图 10 中的阶段 1~7,相应的定子电枢电压与功角的变化规律见表 1。当电机运行至阶段 7 后,由他控给定电压与功角计算得出的电流值与永磁同步电机无位置传感器控制系统的反馈电流相等,此时即开始控制方式由他控向自控的切换。
图 11 给出了他控起动过程中电压空间矢量变化曲线的极坐标。从图中可以看出,电压空间矢量围绕着圆心旋转一周,说明电机的电角度也随之变化了一个周期。由电机极对数 Np=4 易知,电机的机械角度和转轴变化的幅度为1/4 个周期。同时,从图 11 中还可以看出他控方式下电压空间矢量旋转了不到四个周期,说明电机尚未旋转一周即实现了电机的他控起动过程,整个过程所需时间较短。
图 12 给出了 PMSM 无位置传感器控制系统以斜坡与正弦波信号叠加作为输入的估算转子位置及其与实测转子位置之间的误差曲线。其中纵向虚线为控制方式切换的时间点。当电机转速位于低速段时,估算与实测转子位置之间存在较大的误差,只能采用他控方式实现电机的零速起动以及正反转状态切换;而当电机转速逐渐上升后,估算转子位置与实测转子位置之间的误差迅速减小,此时切换为自控方式对电机实施高精度调速。
从图 13 给出的估算转子位置和实测转子位置曲线的局部放大图可以看出,当电机转速较低时,转子位置角度增大的速度较慢,在图中体现为锯齿波的排列较稀疏;而当电机转速升高时,转子位置角度增大的速度也随之变快,此时在图中则体现为锯齿波的排列较密集,符合电机转速由零升高到峰值并再次回到零的转子位置变化规律。
6 结论
针对无位置传感器永磁同步电机控制系统中电机低速时无法准确获取系统参数以及由此而导致电机无法零速起动的问题,利用变压变频控制策略进行他控起动,结合滑模观测器对于转子角度和转速的预测功能,依据电流跟随和转速跟随的原则,使用时变滑模控制器实现控制系统由他控方式向自控方式的切换。仿真和实验证明,本文提出的控制策略不但解决了无位置传感器控制方式下的控制死区问题,而且较好地实现由他控方式向自控方式的平滑过渡,达到较高的综合控制性能。——论文作者:陈思溢 1 皮佑国 2
参考文献
[1] 王庆龙, 张崇巍, 张兴. 基于变结构模型参考自适应系统的永磁同步电机转速辨识[J]. 中国电机工程学报, 2008, 28(9): 71-75. Wang Qinglong, Zhang Chongwei, Zhang Xing. Variable-structure MRAS speed identificati on for permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2008, 28(9): 71-75.
[2] 胡维昊, 王跃, 李明烜, 等. 基于 MRAS 的多相永磁直驱型风力发电系统无速度传感器控制策略研究[J]. 电力系统保护与控制, 2014, 42(23): 118-124. Hu Weihao, Wang Yue, Li Mingxuan, et al. Research on sensorless control strategy of direct drive multi-phase PMSG wind power generation system based on MRAS[J]. Power System Protection and Control, 2014, 42(23): 118-124.
[3] Ohara M, Noguchi T. Rotor position sensorless control and its parameter sensitivity of permanent magnet motor based on model reference adaptive system[J]. IEEE Transactions on Industry Applications, 2012, 132(3): 426-436.
[4] Gao Wei, Guo Zhirong. Speed sensorless control of PMSM using model reference adaptive system and RBFN[J]. Journal of Networks, 2013, 8(1): 213-220.
[5] 周扬忠, 林启星, 马俊亭. 凸极式永磁无刷直流电机无位置传感型瞬时转矩观测[J]. 中国电机工程学报, 2013, 33(18): 87-95. Zhou Yangzhong, Lin Qixing, Ma Junting. Instantaneous torque estimation in sensorless saliency permanent magnet brushless DC motors[J]. Proceedings of the CSEE, 2013, 33(18): 87-95.
[6] 周永勤, 王旭东, 张玉光, 等. 开关磁阻电机模糊滑模观测器间接位置检测[J]. 电机与控制学报, 2013, 17(6): 57-63. Zhou Yongqin, Wang Xudong, Zhang Yuguang, et al. Sensorless detection technique on fuzzy sliding mode observer for SRM[J]. Electric Machines and Control, 2013, 17(6): 57-63.
[7] 辛凯, 詹琼华. 基于滑模观测器的开关磁阻电动机间接位置检测技术研究[J]. 微电机, 2007, 40(9): 9-13. Xin Kai, Zhan Qionghua. Sensorless control of switched reluctance motor driver based on sliding mode rotor position observer[J]. Micromotors Servo Technique, 2007, 40(9): 9-13.
[8] 张旭龙, 谭国俊. 在线建模的开关磁阻电机四象限运行无位置传感器控制[J]. 电工技术学报, 2012, 27(7): 26-32. Zhang Xulong, Tan Guojun. Four-quadrant position sensorless control of switched reluctance motors based on on-line modeling[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 26-32.
转载请注明来自:http://www.lunwencheng.com/lunwen/dzi/21797.html