摘要为研究竹集成材(LBL)钉节点顺纹向受力时的承载性能、变形特性和破坏机理,对125个钉节点双面剪切试件进行了单调静力加载破坏性试验,研究参数包括钉直径、列数和行数.试件的破坏主要有钉帽下部的竹材局部压屈、销槽承压破坏、双铰破坏及LBL劈裂破坏.钉节点的抗剪承载力随钉子直径、列数和排数的增加而增大,但群钉节点的承载力明显小于单钉节点的承载力之和.提出并验证了群钉节点的有效钉子数量和销槽承压有效长度系数计算公式,对比分析了4种常见的屈服点确定方法,结果表明5%钉直径偏移法更适合预测LBL钉节点的屈服荷载.
关键词竹集成材;钉节点;抗剪性能;有效钉子数;销槽承压有效长度系数;屈服点
目前,发展低碳经济正逐渐成为一种新的国际潮流,也是实现未来可持续发展的必然选择.我国的竹子种植面积、蓄积量和加工水平位居世界前列,先后开发出竹胶板、竹集成材(laminatedbam‐boolumber,LBL)和重组竹等竹质工程材料[1-4],克服了圆竹尖削度高、壁薄中空和霉变等缺陷[5],产品品种已经系列化和标准化.作为一种生态环保型的绿色建材,LBL的力学性能明显优于圆竹和普通木材,已成为土木工程新型结构材料研究的热点.尽管LBL在房屋和桥梁等结构中已有一定的应用,但其设计和建造过程仍然采用木结构设计标准,制约现代竹结构在土木工程领域推广应用的“卡脖子”问题亟待解决.
节点主要起到承担并传递荷载及保证结构整体稳定性的作用,其性能直接关乎结构的安全性和可靠性,是结构设计中的关键环节.常见的连接形式包括榫卯连接、齿板连接、植筋连接和销连接(钉、螺栓和销钉)等.其中钉节点具有构造简单、施工方便和成本低等优点,被广泛应用于现代木结构中.相比木结构钉连接,LBL钉节点具有更高的承载力和刚度,能够满足现代竹结构对节点的要求.尽管文献[6-8]对竹结构销连接的性能进行了初步的探讨,但其破坏机理和荷载-滑移关系仍不明确.国内外研究者针对木结构销连接的抗剪性能开展了大量的试验和理论分析[9-11],探讨了影响木结构销连接力学性能的关键参数并基于试验数据得到了承载力计算公式,为LBL钉节点的研究提供了有益的参考.文献[12-13]对木结构销连接的构造要求提出了具体的规定,同时建议了相应的设计计算方法,但并不涉及工程竹材的钉节点.
本研究以钉直径、钉子的行数和列数为主要参数,开展LBL钉连接节点的抗剪试验,考察各参数对试件承载能力、刚度、延性等的影响,研究群钉折减系数,对比分析不同国家规范中的屈服点确定方法,并在试验的基础上提出承载力计算公式,以期为此类钉节点的设计应用提供设计依据和参考.
1材料及方法
1.1试验材料
本试验对LBL的顺纹向的力学性能进行测试,含水率平均值为9.2%,比重平均值为0.78,抗拉强度、抗压强度、弹性模量的平均值分别为107.7MPa,56.3MPa和11GPa.试验用铁钉为普通光圆杆,实测其抗弯强度平均值为705.2MPa.
1.2试件设计
钉连接常用于LBL构件的接长或搭接,为了解现代竹结构建筑中的钉连接的受力性能,本试验参照实际工程案例的做法,LBL钉节点由两块边部构件和一块中部构件通过钉子按照一定的间距连接而成.边部构件和中部构件的截面尺寸分别为20mm×40mm和40mm×40mm,长度L均为150mm,如图1所示.采用射钉枪的方式打钉操作简便,可大大降低工人的劳动强度,但打钉过程中极易劈裂LBL构件[14],因此先用电钻在LBL构件的相应位置钻孔,孔径约为钉直径的80%左右,钻孔深度约为钉长度的90%左右.
相关知识推荐:如何给期刊投稿学术论文
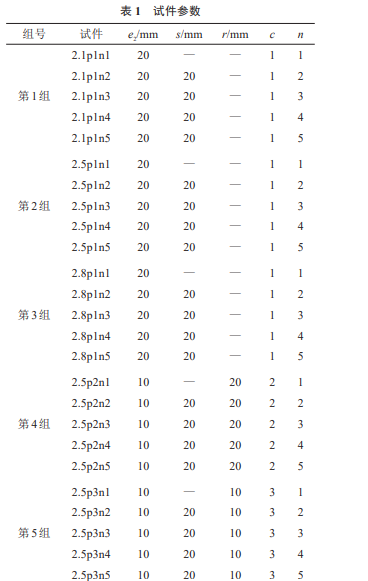
设计了25组试件,每组的重复试件数为5个,共125个钉节点试件,各组试件尺寸详见表1,表中:e2为边距;s为中距;r为行距;c为钉子列数;n为单列钉子中的个数.第1组试件所采用的钉直径D=2.1mm,钉长度l=40mm;第2,4和5组试件所采用的钉直径D=2.5mm,钉长度l=50mm;
第3组试件所采用的钉直径D=2.8mm,钉长度l=60mm.第1,2和3组研究钉直径D和单列钉子中的个数n的影响;第4和5组研究钉子列数c的影响.其中编号为2.1p1n1的试件表示钉直径D=2.1mm,1列钉子,每列1个,如图2(a)所示;编号为2.5p2n5的试件表示钉直径D=2.5mm,2列钉子,每列5个,如图2(b)所示.
文献[8]对LBL钉节点的构造要求进行了初步探讨,结果表明:当钉间距满足最小构造要求时,即端距e1≥6D,边距e2≥4D,行距r≥3D,中距s≥6D时,钉节点将发生延性破坏.本次试验的钉间距均满足最小构造要求,其中端距e1=20mm.
1.3试验加载及测试
试验采用最大负荷量程为5t的作动器对试件施加竖向荷载,如图3所示.为防止试件在加载过程中出现平面外的破坏,在边部构件的底部中间放置一个15mm×40mm×40mm的LBL垫块,并在试件底部安装一个C型夹具.在试件两侧分别安装一个位移计以测量中部构件和边部构件的相对竖向位移.采用位移控制的方式匀速加载,加载速率为1.5mm/min.量测的内容包括作动器荷载及边部构件和中部构件的相对滑移.荷载和相对位移数据由DH3820静态应变测量系统采集.
2结果与讨论
2.1破坏模式
钉节点的破坏形态与钉直径、行数和列数相关.加载初期,钉子与孔壁存在间隙,钉子并非同时受力,节点表面无可见破坏,但偶尔可听见细小的竹纤维断裂声.随着荷载的持续增大,钉子同时承受剪力和拉力,由于钉帽和钉杆塑性变形而产生的“绳索效应”将阻止边部构件和中部构件的相对竖向滑移.单钉节点及部分群钉节点中,当钉子受到的拉力超过竹材的横纹承载力时,易首先发生钉帽下部的竹材局部压屈,如图4(a)所示.当钉子正下方的竹纤维受到的压应力超过竹材顺纹销槽承压强度时,边(中)部构件将发生销槽承压破坏.随着荷载的递增,绝大部分钉节点试件的销槽附近微裂缝进一步向构件底部发展,与此同时钉子在边(中)部构件内逐渐形成2个塑性铰(图4(b)),即双铰破坏.对于部分群钉节点而言,销槽底部的纵向裂缝在加速破坏阶段快速向构件端部发展并最终导致边部构件或中部构件被劈裂,如图4(c)所示.但是在节点发生纵向劈裂破坏前,LBL构件的销槽和钉子均发生了明显的双铰破坏.
2.2荷载-滑移关系
图5为编号为2.8L1R1的试件的荷载(F)-滑移(Δ)曲线.加载初期中部构件和边部构件间将产生一定的相对滑移,但荷载增幅较小,这主要归因于钉子和钉孔间的空隙导致各个钉子无法同时充分发挥其相应的承载能力.靠近LBL端部的钉子首先承受外荷载,其余钉子再依次受力,节点内的钉子受力不均,具体表现为端部钉子承受的荷载较大,而中部钉子受力较小,这种类似的现象亦发生在木结构销连接试验中[15-16].当荷载从10%Fm(Fm为极限荷载)到40%Fm~50%Fm时,荷载与位移基本呈线性变化,各个钉子承担的荷载逐渐趋于均匀.随着荷载增加,节点进入弹塑性阶段,竹纤维开始发生断裂,部分荷载-滑移曲线表现出明显的锯齿形,这主要是因为钉子被间断地拔出所致.节点进入加速破坏阶段,荷载值仍然持续增加,但荷载增长速率明显放缓,相对滑移数值增长越来越迅速,然而部分试件的滑移超过15mm后,其承载力仍未发生下降.
3承载能力分析
3.1极限承载力
根据文献[17]的相关规定:若荷载-滑移曲线上峰值荷载对应的滑移值≤15mm,则取该峰值荷载值作为节点的极限荷载值Fm;若峰值荷载对应的滑移值>15mm,则取滑移值为15mm时所对应的荷载值为Fm.钉直径对试件的极限承载力有着显著的影响,直径越大,试件承载力越高,如图6所示.2.1p1n1,2.5p1n1,2.8p1n1分别对应直径为2.1,2.5,2.8mm的单钉节点,其极限承载力平均值分别为3.14,4.01,5.75kN.2.5p1n1和2.8p1n1的极限承载力较试件2.1p1n1分别提高了27.71%和83.12%.
2.5p1n5,2.5p2n5和2.5p3n5的试件中,每列包含5个直径为2.5mm的钉子,列数分别为1列、2列和3列.多列钉子的节点的承载力近似等于单列钉子的承载力与钉列数的乘积.以第1组试件为例,2.1p1n1,2.1p1n2,2.1p1n3,2.1p1n4和2.1p1n5为仅包含单列钉子的试件,分别有1~5排(个)钉子,其承载力分别为3.14,5.43,7.34,10.93,11.79kN.节点的极限承载力随钉子排(个)数的增加而增加,但是群钉节点的承载力并不是单钉节点的承载力简单叠加,而是小于单钉节点的承载力与钉排(个)数的乘积,因而须要考虑群钉节点的折减系数.
4结论
a.LBL钉节点受剪破坏形态有钉子穿透边部构件、销槽承压破坏、边(中)部构件内钉子形成塑性铰和劈裂破坏4种,表现出典型的延性破坏特征.前2种破坏形态主要出现在节点破坏的前期,第3种是主要的破坏形态.在试件加速破坏的后半段,部分钉节点将发生劈裂破坏,而这种现象通常也发生在木结构销连接脆性破坏的实验中.
b.钉节点荷载-位移曲线可划分为4个阶段:初始滑移阶段,线弹性阶段,弹塑性阶段,加速破坏阶段.荷载-位移曲线无明显屈服点,采用K&C,CEN和CSIRO法明显高估了钉节点的屈服点,而5%D法更加符合实际情况,可以很好地确定LBL钉节点的屈服荷载.
c.在试验研究与分析的基础上,给出了LBL钉节点承载力计算公式,承载力由屈服模式Ⅳ所决定,这与实测观察到的屈服模式Ⅳ相符合.提出的基于屈服模式Ⅳ的推导公式的理论计算结果与试验值符合良好.——论文作者:陈国a,b吴静b谈闯b于云飞b
转载请注明来自:http://www.lunwencheng.com/lunwen/lig/20144.html