摘要:土体空间变异性分析是进行岩土工程可靠度设计的理论基础。采用随机场理论,提出了典型江苏海相黏土的随机场特征及参数,对基于孔压静力触探(CPTU)测试数据的空间变异性进行了系统分析。由于竖直方向上CPTU锥尖阻力数据的样本容量较高,通过对锥尖阻力进行一次多项式去趋势来获得平稳的波动分量,并利用常用的5种自相关模型拟合波动分量的自相关系数。采用修正的Bartlett统计公式来检验波动分量的平稳性,选取最优的竖直波动范围。竖直变异系数由波动分量和去趋势函数来确定。鉴于水平方向上的CPTU锥尖阻力数据的样本容量较小,采用平均零跨距法估计水平波动范围,水平变异系数由总体变异系数来表示。结果表明,竖直向和水平向上江苏海相黏土较报道值显示出更强的空间变异性。
关键词:空间变异性;海相黏土;孔压静力触探;随机场理论
0引言
天然沉积土是在漫长的地质年代中形成的,由于形成过程中受搬运、沉积和风化等各种作用产生复杂的物理化学反应,使得土体岩土工程参数具有显著的空间变异性。对土体岩土工程参数的空间变异性分析是进行岩土工程可靠度设计的理论基础,目前常采用随机场理论对岩土工程参数的空间变异性进行分析,定量研究其变化规律。国内外许多学者基于随机场理论对各种不同场地条件或地质成因土体的空间变异性进行广泛的研究。
Vanmarcke[1-2]首先系统地阐述了随机场理论并将其应用于岩土工程参数的空间变异性研究中。Phoon等[3-5]基于大量的室内试验、现场测试和文献资料,将常用的岩土工程参数指标的空间变异性进行汇总并提出了修正的Bartlett检验。Jaksa等[6-7]给出了5种最适合岩土参数的自相关函数模型并研究了Keswick黏土在不同取样间距下的波动范围的变化规律。Uzielli等[8]对土耳其和北美5个试验场地的CPTU测试资料进行了不同土类的空间变异性研究,利用线性回归方法拟合趋势项,采用自相关函数方法计算波动范围,并对波动分量平稳性进行修正的Bartlett检验。Stuedlein等[9]对贝城干燥黏土的CPTU数据进行分析研究了趋势项函数和自相关模型对波动范围的影响,并获得贝城干燥土空间变异性参数。高大钊[10]研究了岩土参数的变异性及其分布规律,包承纲[11]、冷伍明等[12]和李小勇等[13]分别对不同地区岩土参数空间变异性参数进行了研究和统计归纳。闫澍旺等[14-15]采用静力触探曲线对土体参数随机场模型的平稳性和各态历经性进行了检验并研究了计算土体参数波动范围的方法。刘润等[16-17]将空间随机场模型应用于海洋结构物地基可靠度分析中,并研制了“海洋土地基可靠度分析系统”。Liu等[18]对园林液化地区的CPT测试资料进行了分析,采用自相关函数方法绘制不同间距的样本自相关函数,求解水平向波动范围,随后采用Monte-Carlo模拟未采样点的数据,利用自相关函数方法求解水平向波动范围。李典庆等[19]、祁小辉等[20]、蒋水华等[21]采用数值模拟方法模拟岩土工程参数的空间变异性并分析了不同空间变异性参数对边坡稳定性的影响。
在进行岩土工程可靠性分析时,参考已有文献资料提出的相似土体空间变异性参数[3,9],对于一般的岩土工程来说,这种工程类比经验是合理的。但是对于具有特殊性质的地区性土体,如江苏地区典型的海相黏土等,这种工程类比经验往往会带来较大误差。本文基于CPTU现场测试数据,采用随机场理论对江苏地区的海相黏土进行空间变异性研究,计算分析了竖直方向和水平方向江苏海相黏土的随机场模型参数及其变化规律,为相似工程条件下的岩土工程可靠度设计理论提供有益的空间变异性参数。1场地描述江苏海相黏土广泛分布于兴华—阜宁—灌南一线以东的苏北滨海平原地区,主要地貌为盐化平原、盐田和海湾低平原。受第四纪以构造影响,地壳剧烈升降;加之古气候频繁周期性冷暖变化,沿海地区发生了多次海侵、海退现象。相关资料显示,江苏东部沿海地区平原第四系发育5个以上海侵层,沉积有厚层的松软黏性土,具有高含水率、高孔隙比、高压缩性、低强度和低渗透性的特点[22]。
试验场地位于连云港—盐城铁路(连盐铁路)灌云段K119+750处,CPTU孔沿路基中心线两侧布置,共进行9孔CPTU试验,布孔位置如图1所示。试验设备采用多功能数字式车载CPTU系统,探头规格符合国际标准,贯入速率为2cm/s,采样间隔0.05m。
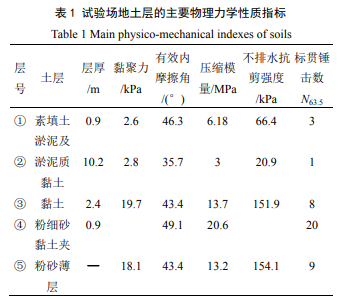
采用基于CPTU试验数据的实用土分类方法[23-24]对CPTU试验结果进行土层分类,典型CPTU测试土层分类结果如图2所示,主要物理力学性质指标见表1。地面表层存在一定厚度的硬壳层;硬壳层以下为淤泥及淤泥质黏土层,以海积沉积作用为主,冲海积为辅,具有含水率高、孔隙比大、低强度、高塑性、黏粒含量高和一定的流变性等特点;其下为强度较高的硬泥层,以黏土、粉质黏土为主并夹有粉细砂。本文主要研究对象为海相沉积和冲海相相沉积形成的淤泥及淤泥质黏土层。
2随机场理论
2.1随机场模型
土体岩土工程参数的空间变异性可以采用统计学的回归分析、随机场理论和地质统计学模型进行分析[25]。由于随机场理论模型及参数可以为岩土工程可靠度分析提供有效的参考依据,其正成为研究土体空间变异性的有力工具,目前广泛应用的是Vanmarcke提出的有限规模的随机场模型[1-2]。
随机场理论利用土体岩土工程参数的空间性,即在给定场地的空间范围内土体岩土工程参数的变化在一定的波动范围内呈现出自相关性,对土体岩土工程参数的空间变异性进行建模分析[7,26]。
土体岩土工程参数的空间变异性可以用随机场模型参数的均值,波动范围和变异系数来描述。应用随机场理论来获得土体空间变异性特点的先决条件是对原始测试数据进行处理以获得零均值的平稳性或弱平稳性随机数据。去趋势方法是最常用的获得平稳随机场的方法,一方面满足随机场理论中对零均值平稳性的要求,另一方面避免由于采用参数总变异性分析而导致高估土层的变异性[28]。
通常,土体岩土工程参数的变异系数定义为其标准差与其平均值的比值。大部分空间变异性文献资料中给出的土体岩土工程参数的变异系数均采用总变异性分析法。总变异性分析法未去除土体参数剖面中潜在确定的趋势项,使所获得的变异系数值可能远大于其空间变异性的真实值。随机场理论中,Phoon等[3]指出应当通过分量分析法,即采用波动分量的标准差和趋势函数的平均值来获得更为合理的土体参数的变异系数。
2.2修正的Bartlett平稳性检验
早期波动分量的平稳性检验中,采用直接观察法或经典的统计学方法[6,9,30]。常用的经典统计检验方法有F检验、Hartley检验和Kendall检验等。然而这些检验方法均假设测试数据之间具有独立性,这与土体岩土工程参数具有空间相关性的事实不相符。故当采用上述方法对具有相关性的测试数据进行平稳性检验时,会产生很大程度的偏差,对测试数据的平稳性产生偏于不保守估计[28,31]。目前广泛采用的是Phoon等[4-5]提出的修正的Bartlett检验,其适用于岩土工程参数数据的平稳性检验[9,32]。
修正的Bartlett检验将随机场模型的测试数据去趋势化、波动范围求解、波动分量平稳性检验以及土层边界识别等内容紧密地联系起来。对波动分量进行修正的Bartlett检验时,需要产生Bartlett检验统计量。
3竖直向空间变异性分析本文以9个孔多功能CPTU试验的锥尖阻力数据为基础,采用随机场理论建立江苏海相黏土竖直方向上的随机场模型,以获得其空间变异性变化规律,计算步骤如下:①数据去趋势处理以获得波动分量;②确定自相关函数及其波动范围;③采用修正的Bartlett检验平稳性;④估计土体的竖直向变异系数。
3.1测试数据去趋势处理
对CPTU试验数据而言,通常采用多项式进行趋势函数拟合来获得波动分量(残差),最常用的是一阶多项式或二阶多项式[8,25]。当趋势函数模型发生改变时,波动分量的方差及自相关结构也会发生变化[33]。许多文献资料指出,随着多项式的阶数增加,对样本数据的拟合效果增强,波动分量的方差和自相关性降低。然而当采用高阶多项式趋势函数时,阶数越高,多项式系数样本方差就越大,从而产生明显的估计误差[5,34-35]。
因此,在实际计算中,建议首先采用线性趋势函数来获得波动分量,当波动分量不满足修正的Bartlett检验的平稳性要求时,再采用更高阶的多项式拟合。本文采用一阶多项式进行趋势项拟合来获得波动分量,如图5所示。
通过拟合结果表4和图6可看出,一次多项式去趋势方法已经能获得足够平稳或弱平稳的随机波动分量。锥尖阻力波动分量的自相关系数在Br=0.14之前显示为迅速衰减的自相关性,该计算结果也与其他文献资料的计算结果相符合[5,9],并且在7t=0.35m处越过Bartlett极限值。每个自相关模型对CPTU锥尖阻力数据波动分量自相关系数的拟合程度均大于0.9。
3.3平稳性检验
土体的均匀性与其岩土工程参数的统计学平稳性等价。从土体物理属性出发,统计学平稳性存在的原因在于测试数据来源于经历了相似的地质历史和成因的均匀土体,具有相似的平稳性。采用修正的Bartlett检验用方法进行土体波动分量平稳性检验时,在不均匀土层交界处,由于土性指标存在突变;反映在统计学特征上则是土体岩土工程参数的波动分量在该交界处附近的局部均值不再保持常量,此时不满足平稳性要求。因此,Bartlett统计量剖面上出现突变点,使得Bstat>Bcrit,即该边界处的土体不满足均匀性要求。
表3表示的修正Bartlett检验的极限值对于5个自相关函数模型来说并不统一。通常,对于土体原位测试数据的平稳性要求的严格程度低于对土体变异性理论研究的平稳性要求。因此,在某些情况下可以采用适当放松的修正的Bartlett检验的极限值[5,9]。
图7为CPTU锥尖阻力波动分量自相关系数的SNX、SQX、CSX、SMK和BIN5种自相关模型的修正的Bartlett检验结果。检验结果表明有SQX、CSX、SMK和BIN4种自相关模型通过了平稳性检验,只有SNX自相关函数模型没有通过修正Bartlett检验。一般的,SNX模型具有最严格的平稳性检验。这表明SNX自相关函数模型可以很好拟合CPTU锥尖阻力波动分量的自相关系数,但是,在该自相关函数的条件下,CPTU锥尖阻力的波动分量表现为非平稳性数据,不能反映土体的岩土工程参数真实的波动变化情况。SQX、CSX、SMK和BIN4种自相关函数模型则可以较好反映土体的岩土工程参数真实的波动变化情况。但是SQX、CSX、SMK和BIN4种自相关函数模型对CPTU锥尖阻力波动分量的自相关系数的拟合程度是不同的。在确定土体竖直向波动范围时,选择自相关函数拟合程度最好的,即表4中相关系数最大的自相关函数模型所对应的竖直向波动范围。
3.5竖直向随机场模型参数
分别对9个孔CPTU试验的锥尖阻力数据进行上述的随机场模型参数计算,可获得江苏海相黏土竖直向空间变异性的变化规律,计算结果见表5。计算结果表明,CPTU锥尖阻力平均值的变化范围为0.38~0.77MPa,平均值为0.52MPa;该结果与文献资料[3]所述黏土的范围一致,且平均值更接近于其所述变化范围的下限。
相关知识推荐:论文发表被拒要不要申诉
采用通过修正的Bartlett检验的自相关函数模型来确定CPTU锥尖阻力的竖直向波动范围。分析9个钻孔的计算结果见表5,没有单一的自相关函数模型适合江苏海相黏土的随机场结构。在某些情况下,通过修正的Bartlett检验的自相关函数模型不止一个,则选取最优相关系数的自相关函数来确定竖直方向的波动范围。江苏海相黏土层竖直方向的波动范围的变化范围为0.27~0.48m,平均值为0.40m;变化范围落于文献资料[3]所述范围。对于江苏海相黏土来说,其竖直方向的变异系数变化范围为3.87%~10.92%,平均值为7.34%,变异程度超出文献资料[3]报道黏土的变异系数变化范围,显示出较强的变异性。
江苏海相黏土高度的空间变异性可能与其形成的地质背景有关,由于受到多次海侵、海退的影响,该黏土的沉积环境多次发生变化,形成的土体物理力学性质也随之发生改变,从而导致其变异系数增大。
4水平向空间变异性分析
4.1CPTU数据处理
水平向随机场参数也是描述土体空间变异性的重要指标,但获得土体水平方向的波动范围和变异系数比较困难。通常情况下水平方向上的取样间距较大,难以获得大容量的样本数据,不能用严格的自相关函数拟合法来计算其水平随机场模型及参数。因此,确定土体的水平向随机场参数的方法与确定土体的竖直向随机场参数的方法并不相同。
锥尖阻力水平向趋势函数只用来确定水平波动范围。水平变异系数采用锥尖阻力的总体变异性来表示。如果采用去趋势后的波动分量来确定变异系数,由于较小样本容量的限制,去趋势产生的波动分量可能会导致错误的协方差估计从而低估土体参数样本数据的变异性,高估样本数据的独立性[37]。
水平方向上钻孔间距小于20m即认为锥尖阻力数据有效。由于水平方向上CPTU钻孔不处于一条直线上,故将二维分布的锥尖阻力数据转化为转化一维径向表示[9]。径向距离为当前选定钻孔至其它观测值钻孔的水平直线距离。
4.2水平随机场模型参数
考虑到每个钻孔的土层厚度各不相同和钻孔间距,如图1所示,只选用CPTU-7、3、5、6、8和9孔的2~10m深度内的锥尖阻力数据进行分析。观察6个钻孔161个相同水平上的锥尖阻力值,其没有显示出随钻孔距离变化的偏差或者异方差性,故认为CPTU锥尖阻力数据是平稳性数据,可采用平均零跨距法计算各深度的水平波动范围。图9为深度3m处的计算结果。在某些情况下,CPTU锥尖阻力曲线与趋势项函数只有两个交点,此时会过高估计其水平向波动范围。——论文作者:林军1,2,蔡国军*1,2,邹海峰1,2,刘松玉1,2
转载请注明来自:http://www.lunwencheng.com/lunwen/nye/22122.html