摘要:磁流体动力学陀螺仪不存在传统陀螺仪的机械磨损和光学陀螺仪寿命易受光学器件制约的缺点,因而具有高精度、宽频带、长寿命的特点,此外还具有抗冲击、体积小、重量轻等综合性能。该传感器不但在惯性导航中表现优异,同时在卫星微角振动测量及寻北等领域也具有广阔的应用前景。通过对磁流体动力学陀螺仪基本工作原理进行简要分析,对简化模型进行了推导,并提出一种磁流体动力学陀螺仪的结构设计方法;对磁路进行仿真,获得工作间隙处磁感应强度分布,并代入磁流体仿真环节;对流动进行仿真,同时对样机进行标定实验,可得出标定过程的仿真与实验间差值的平方和均值的开方为5.69 mV,非线性度为0.6%,表明通过研究导电流体的流动过程进而分析该陀螺仪的性能是十分必要的,并证明了磁流体动力学陀螺仪具有良好的发展前景。
关键词:磁流体动力学;结构设计;仿真和实验
1 引 言
陀螺仪是惯性导航中最重要且技术含量最高的元件,用于检测载体的角运动,其综合性能对惯性导航系统的整体性能有直接的决定作用。然而现有陀螺仪㈣3存在诸多问题:基于进动的动力调谐陀螺仪㈨存在无法克服的触点磨损,液浮陀螺仪和静电陀螺仪…3制作加工工艺复杂;基于干涉的光学陀螺仪…的寿命受到光源和光学器件的限制;基于柯氏效应的MEMS陀螺仪…精度难以提高。尽管陀螺仪的加工和制造工艺已有较高水平,但无论是传统的机械陀螺仪还是基于新原理的光学、 MEMS和原子陀螺仪,在精度、频带、体积和寿命等综合性能的提升方面都存在极大困难,这极大制约了相关领域的发展,如具有宽响应范围的高精度卫星姿态及平台振动测量技术¨1,其稳定度就是由装载于飞行器的陀螺仪的精度和带宽所制约。我国航空航天技术的发展,对陀螺仪性能和适用场合提出的要求也越来越苛刻,亟需开发综合性能优异的新型陀螺仪。
磁流体材料具有优良的电磁学和机械流变属性,具有屈服强度高、动态特性好、阻尼调节范围宽等优点。磁流体动力学陀螺仪主要是利用了磁流体导电的特性,其基本思想运用了电磁感应的原理。相较于传统陀螺仪,克服了摩擦阻尼和磨损的难题;提高了使用寿命,抗过载能力;兼具高精度、宽频带、小型化、长寿命、低成本,对加速度冲击不敏感,适合苛刻条件下工作等特点,适合大规模的集成制造。美国ATA(applied technology associates) 公司在20世纪80年代末就开始研究磁流体动力学陀螺仪一。1…,技术趋于成熟,并已实现产业化…。1…。以该公司典型产品ARS一15为例,标度因数为1 V/(tad·S“),非线性度小于0.25%。由于国外技术封锁及产品禁运,国内磁流体动力学陀螺仪的发展较为缓慢。2008年,罗荣锋¨41 阐述了磁流体陀螺仪的原理,并分析了水银材料在圆环形玻璃通道内的流速状态,以及适合低精度陀螺仪测试的平台系统方案;2011年,霍红庆等人¨。”1分别论述了磁流体陀螺仪用于惯性微角颤振测量的工作原理、性能指标和应用,理论分析了磁流体陀螺仪需要解决的一些关键技术。整体来说,国内对于磁流体陀螺仪的研究还较少,已远远落后于美国、日本、欧洲等发达国家。
本文提出了一种磁流体动力学陀螺仪的设计方法,包括传感器机械结构以及磁路仿真设计,以及导电流体流动的仿真,最后进行了样机标定实验,实验结果表明该磁流体动力学陀螺仪样机的性能与仿真相符,同时可以很好地敏感角运动信息。
2基本工作原理
磁流体动力学陀螺仪利用了磁流体材料导电的特性,其基本思想是电磁感应的原理。如图1所示,下面的圆柱体为永磁体,产生垂直磁场;上面的圆环为黏度很小的磁流体通道。将其与待测的转动物体固定在一起。
3磁流体动力学陀螺仪结构设计
根据上述磁流体动力学陀螺仪工作原理,设计一种基于该原理的磁流体动力学陀螺仪机械结构,包括了磁流体通道的构建、垂直磁路的设计、磁场屏蔽的方法3部分。其中,最复杂的部分为磁流体通道的构建。磁流体所在通道的上下壁面为绝缘体(见图2中压套1和密封套4),内外壁面为导体(见图2中壳体3芯柱5)。通过对永磁体等组成磁路的零件尺寸和材料的合理选择与设计,为磁流体通道提供垂直磁场。圆柱体外壳选用高磁导率的材料,如此为永磁体形成闭合磁回路,同时也可使外壳内部免受外界杂散电磁场的干扰。外壳内底部放置圆片状永磁体,上面用密封套卡住,防止永磁体与磁流体接触。压套压在芯柱的轴肩与外壳下孔肩上,阻隔芯柱与螺纹压盖防止内外电极短接;螺纹压盖紧压在压套上使芯柱底面与密封套上表面、芯柱轴肩与压套下表面紧密接触,防止磁流体溢出流体通道。螺纹压盖与外壳材料相同,二者螺纹配合,电位相同;螺纹压盖与芯柱分别钻有电极槽,安装电极方便信号处理电路采集流体通道内、外壁电位信号。外壳底面钻有螺纹孔,方便将磁流体动力学陀螺仪固定在被测载体上。
4磁流体动力学陀螺仪磁路分析与仿真
永磁体是提供工作气隙磁能的能源。合理选择永磁体材料m1是磁路设计的一个重要方面。对于永磁材料,在退磁曲线上存在着最大磁能积点,在这点上永磁体体积最小而产生的磁通最大。因此在选择永磁体材料时应考虑最大磁能积(BH)。、剩余磁感应强度日,、矫顽力Ⅳ,、温度系数、最高工作温度等。除此之外还必须考虑磁性材料在冲击、振动、湿热等环境条件下导致的干扰不敏感或敏感度极低。综合各方面因素,最终选择了具有高磁能积和高矫顽力的稀土永磁材料——钕铁硼。
本设计中,工作空间为磁流体通道,要求磁场垂直且均匀,必须兼顾通道高度和磁感应强度这2个因素。保证磁感应强度的前提下,尽量减少工作气隙的高度。工作气隙与永磁体的工作点位置有着密切的关系。为了使永磁体工作点尽量靠近具有最大磁能积点的位置,需要改变工作气隙的结构参数,取得较好的效果。
此外,还必须对磁路进行合理的设计以保证外界磁场不会对内部磁路产生影响,降低传感器精度;同时,传感器不对外产生任何外磁场,不会对其他设备产生磁影响。壳体选用具有高导磁率的镍铁合金材料,一方面使得磁感应线在传感器内构成低磁阻通路,把磁力线封闭在壳体内,从而阻挡内部磁场向外扩散;另一方面外界干扰磁场的磁力线在壳体的外表面处发生畸变,使内表面处及腔内的磁力线密度大为减少,有效抑制外界磁场的干扰。
对设计磁场结构利用有限元进行仿真,模拟的磁通密度矢量图和等值云图如图3所示。由此可看出,本设计不仅能够对工作气隙提供较为垂直均匀的磁场,而且能够有效阻隔外界磁干扰。
5仿真与实验
5.1 陀螺仪内磁流体流动仿真
在磁流体动力学陀螺仪中,磁流体材料所在容器为空心圆柱体,其流动整体表现为绕中心轴的旋转运动。首先简化为开放矩形截面管道的流动。磁流体的流动是由壁面运动引起黏性作用的引射流动。
在研究基于磁流体动力学的传感器时,仿真方法¨“驯多采用有限元法、边界元法、有限体积法等。这里选择有限体积法。该传感器中流体的流动是在封闭矩形截面管道的流动。在实际传感器的使用过程中,@/Oz#O,边界条件不是简单的两个壁面相对滑动的关系,运动方式也更加复杂。本文中通过基于FLUENT软件,对传感器进行了磁流体力学的分析,并进行了流动仿真。根据真实情况,选择了基于电压的模式,还考虑了重力加速度的影响。输入运动方程选择口=sin(20仃£),初始条件定义为O.1个大气压和20℃。对10个周期的运动状态进行仿真和记录。当磁场不存在时,容器内部导电流体的流动状态时无序的,而当磁流体动力学现象存在时,流体的角速度呈现出近似正弦的变化,仿真结果如图5所示。分析通道内任一矩形截面的流速值,由于内外壁与载体固定连接,因而在运动过程中,任意时刻对于同一高度而言,呈现梯形分布;对于同一半径而言,也呈现出梯形分布。
本文来源于:《仪器仪表学报》是中国仪器仪表学会主办,它所刊登的论文代表了中国仪器仪表学科的最高学术水平,反映仪器仪表学科的前沿、研究热点,标志中国仪器仪表学科的发展方向
仿真还需考虑到磁场均匀性的影响。在简化模型的推导过程中磁场采用的是恒定值,然而由磁路仿真得到的磁场并不十分均匀。对这2种情况进行磁流体动力学的仿真,通道内外壁输出电动势的幅值后者比前者约减少10%。此外,根据仿真结果,诱导电流产生的磁感应强度值约为10。T,因而该误差可以被忽略。
5.2标定实验
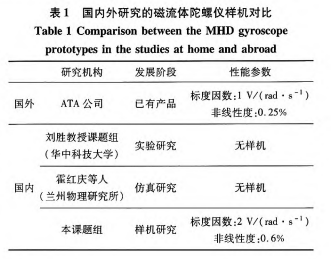
基于上述设计方法制成磁流体动力学陀螺仪样机,如图6(a)右下角所示。将磁流体动力学陀螺仪样机固定于单轴转台上,用信号发生器向转台控制端输入正弦信号使转台模拟角振动,角振动幅度可以根据转台测速电机反馈电压信号计算得到。在示波器上观测磁流体动力学陀螺仪信号处理电路输出信号及转台测速电机反馈电压信号。20℃条件下,输入幅值为0.2~3 V,频率为 1 Hz的控制电压对磁流体动力学陀螺仪进行标定,得到的实验结果如图7(b)所示。经计算可得实际输入输出之间表达式为:U。。=0.297 3 Ui一0.027 9,仿真与实验间差值的平方和均值的开方为5.69 mV,从而得出标度因数为2 V/(rad·S“),非线性度控制在0.6%以内这个结论。从表1中对比可看出,本文设计的磁流体陀螺仪与国外先进水平尚存在一定的差距。
6 结 论
通过对磁流体动力学陀螺仪基本工作原理进行简要分析,对简化模型进行推导,提出一种磁流体动力学陀螺仪的结构设计方法,对磁路和磁流体流动进行仿真,同时进行了标定实验,实验结果表明磁流体动力学陀螺仪能够敏感角运动并且具有较好的线性度。该研究从磁流体动力学基本方程人手,对矩形截面流体通道内磁流体的流动进行了理论、仿真和实验分析,得出磁场的不均匀度是影响输出的一个重要因素,而诱导电场产生磁场的影响十分微弱这些结论。该样机达到惯性导航和微角振动测量还具有一定的距离。
目前研究与国外先进水平的差距体现在:
1)由于加工装配工艺的限制,目前为手工装配,公差配合可能并没有得到严格的保证;
2)对传感器的误差分析尚属初步研究,没有引入误差补偿技术;
3)实验平台限制了技术指标的有效测量。
为提高传感器性能,需要对其进一步研究,包括:
1)将自动化装配应用到传感器的装配中,减少装配过程中带来的误差;
2)对数学模型建立过程中的省略项进行误差分析,引入误差补偿机制;
3)制定适用于磁流体动力学陀螺仪的测试标准和测试方案。——论文作者:徐梦洁1,李醒飞1,吴腾飞1,陈诚2,于翔1
转载请注明来自:http://www.lunwencheng.com/lunwen/dzi/21945.html